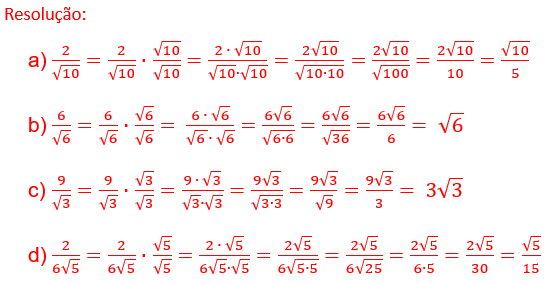Exercícios com o conjunto dos números reais

O conjunto dos números reais () é formado pela união () dos conjuntos numéricos:  racionais () e irracionais (). Pode-se representá-lo, portanto, com a expressão:

 

 =   

Os números naturais são (0, 1, 2, 3, 4, 5 …) e assim por diante. Os inteiros incluem os números negativos (…–3, – 2, –1, 0, 1, 2, 3 …). Os racionais são aqueles que podem ser expressos na forma de fração  , em que "a" e "b" são números inteiros e "b" é diferente de 0 (4, -10, 1/2, 3/4, – 5/4, 0,25 etc.). Os irracionais são os que não podem ser obtidos pela divisão de dois números inteiros (, – , , ou  = 3,141592 …, entre muitos outros). 

Observe que:

1) Todo número natural é inteiro;
2) Todo número inteiro também é racional, embora não seja representado sob a forma de fração. Isso significa que  está contido em  e que  está contido em . Consequentemente,  =   .

Um número irracional importante:

A razão entre a medida do comprimento(C) de uma circunferência e a medida do seu diâmetro(D) obtemos uma constante: o número pi; representado pela letra grega .

Exercícios

1 - O número racional 1/6 é igual a:
a) 1,6

b) 0,6
c) 0,16
d) 0,1666...

Resposta:
Como fração é divisão
1/6 = 1: 6 = 0,1666...

2 - O número 0,212121… é equivalente a:
a) 110/9
b) 21/99

c) 220/9
d) 9/22

Resposta: Para encontrar a fração geratriz dessa dízima periódica, vamos fazer:

x = 0,212121...

Multiplicar por 100 ambos os lados dessa igualdade:

x = 0,212121...   X 100

100x = 21,212121...

Subtraindo 100x - x vamos ter:

3 - O valor da expressão é:

A resposta correta é:

a) é um número irracional.
b) não é um número inteiro.
c) é um número real.
d) não é um número racional.

Resposta:

4 - Observe o conjunto A e responda:

A resposta correta é:
(a) e (e)
(b) e (d)
(c) e (d)
(d) e (e)

Resposta:

Valor numérico de uma função quadrática

Para encontrar o valor numérico de qualquer função, basta substituir a variável independente pelo valor desejado e encontrar o valor da variável dependente.

Neste caso, temos a função:

y = 2x² – 3x + 5

Onde y é a variável dependente, também conhecida como f(x), e x é a variável independente.
Substituindo x pelo valor – 2:
y = 2⋅(– 2)² – 3⋅(– 2) + 5

Substituindo x pelo valor – 1:

y = 2⋅(– 2)² – 3⋅(– 2) + 5
y = 2⋅(– 2)⋅( – 2) + 6 + 5
y = 2⋅4 + 6 + 5
y = 8 + 6 + 5
y = 19

 Exercícios

 1 - Calcule o valor f(2) na função f(x) = x² – 4x + 7.

a) f(2) = 1
b) f(2) = 2
c) f(2) = 4
d) f(2) = 3

 Resposta: 

f(2) = 2² – 4⋅2 + 7
f(2) = 2⋅2 – 4⋅2 + 7
f(2) = 4 – 8 + 7
f(2) = – 4 + 7
f(2) = 3

 2 - Determine o valor de y para x = 3 na função quadrática, cuja a lei de formação é y = 2x² + 5x – 3.

a) f(3) = 40
b) f(3) = 30
c) f(3) = 35
d) f(3) = – 20

 Resposta: 

y = 2⋅3² + 5⋅3 – 3
y = 2⋅3⋅3 + 15 – 3
y = 2⋅9 + 15 – 3
y = 18 + 15 – 3
y = 33 – 3
y = 30

 3 - Dada a função f(x) = – x² – 2x + 4, determine o valor de f(5).

a) f(5) = 32
b) f(5) = 31
c) f(5) = – 32
d) f(5) = – 31

Resposta: 

f(5) = – 5² – 2⋅5 + 4
f(5) = – 5⋅5 – 10 + 4
f(5) = – 25 – 10 + 4
f(5) = – 25 – 10 + 4
f(5) = – 35 + 4
f(5) = – 31

4 - Dada a função f(x) = x² – 4x + 3, determine o valor de f(– 2).

a) f(– 2) = – 15
b) f(– 2) = 16
c) f(– 2) = 15
d) f(– 2) = 14

 Resposta: 

f(– 2) = (– 2)² – 4⋅(– 2) + 3
f(– 2) = (– 2)⋅(– 2) + 8 + 3
f(– 2) = 4 + 8 + 3
f(– 2) = 15

Exercícios com função do 1º grau

Uma função do 1º grau pode ser escrita na forma:

f(x) = ax + b    ou    y = ax + b, sendo os coeficientes "a" e "b" números reais, com a ≠ 0 e "x" é a variável. 

Exercícios:

1 – (UERJ) A promoção de uma mercadoria em um supermercado está representada, no gráfico a seguir, por 6 pontos de uma mesma reta. 

Quem comprar 20 unidades dessa mercadoria, na promoção, pagará por unidade, em reais, o equivalente a:

a) 4,50
b) 5,00
c) 5,50
d) 6,00

Solução: 

Temos os pontos P(5, 150) e Q(30, 50). Como o gráfico é uma reta, a função é do 1° grau:

y = ax + b
150 = a⋅5 + b  ⇒   5a + b = 150 (1)
50 = a⋅30 + b  ⇒  30a + b = 50 (2)
Isolando b em (1):
5a + b = 150  ⇒  b = 150 – 5a (3)
Substituindo b em (2):
30a + b = 50
30a + 150 – 5a = 50
30a – 5a = 50 – 150
25a = – 100 ∴ a = – 4
Substituindo o valor de a em (3):
b = 150 – 5a   ⇒   b = 150 – 5⋅(– 4)
b = 150 + 20 ∴ b = 170
Para x = 20 unidades:
y = ax + b  ⇒  y = – 4x + 170
y = – 4⋅20 + 170  ⇒  y = – 80 + 170 = 90
Preço por unidade: 90:20 = 4,50

2 – (PUC-BH) A função linear R(t) = at + b expressa o rendimento R, em milhares de reais, de certa aplicação. O tempo t é contado em meses, R(1) = – 1 e R(2) = 1. Nessas condições, determine o rendimento obtido nessa aplicação, em quatro meses. 

Resolução:

R(1) = – 1

R(t) = at + b

R(1) = a⋅1 + b = – 1   ⇒   a + b = – 1 (1) 

R(2) = 1

R(t) = at + b

R(2) = a⋅2 + b = 1   ⇒    2a + b = 1 (2)

Isolando b em (1):
a + b = –1 ⇒ b = –1 – a (3)

Substituindo (3) em (2):

2a + b = 1   ⇒   2a + (–1 – a) = 1

2a – 1 – a = 1   ⇒   2a – a = 1 + 1

a = 2 

Substituindo o valor de a em (3):
b = – 1 – a ⇒ b = –1 – 2 ∴ b = – 3

Portanto, a função será:
R(t) = at + b
R(t) = 2t – 3

Fazendo t = 4 meses:
R(t) = 2t – 3   ⇒   R(4) = 2⋅4 – 3

R(4) = 8 – 3   ∴   R(4) = 5

Resposta: O rendimento obtido nessa aplicação será de R$ 5 000,00. 

3  – Identifique quais das funções abaixo são do 1º grau:

a) f(x) = 10x – 12       b) f(x) = 1/x + 8

 c) f(x) = 9x + 3          d) f(x) = 4x² + 3x – 16

 e) f(x) = 5x + 3x³        f) f(x) = 5x – 1

Resposta: As funções que têm a forma f(x) = ax + b são (a), (c) e (f).

4  – Determinando os coeficientes da função y = 2x + 9, vamos ter:

a) a = 2 e b = 9

b) a = 1 e b = 9

c) a = 9 e b = 1

d) a = 2 e b = 11

Resposta: a = 2 e b = 9

5  – Uma função do primeiro grau tem lei de formação dada por y = 2x + 3, qual o valor de x para que y = 13?

a) x = 8
b) x = 12
c) x = 9
d) x = 5

Resolução:

 y = 2x + 3
13 = 2x + 3
13 – 3 = 2x
10 = 2x

x = 5

6 – O problema a seguir, refere-se às questões 4, 5 e 6.

Paulo trabalha como funcionário de uma loja e recebe R$ 1 800,00 todo mês mais R$ 10,00 por cada produto vendido.

Escreva a função que representa seu salário;

a) y = 1 800x + 10

b) y = 10x + 1 800

c) y = (1 800 + 10)x

d) y = 1 810x

 Resposta: y = 10x + 1 800

7 – Se ele vender 42 unidades do produto, quanto vai receber?

a) R$ 2 220,00

b) R$ 3 010,00

c) R$ 1 810,00

d) R$ 2 410,00

Resolução:

x = 42

y = 10x + 1800

y = 10ㆍ42 + 1800

y = 420 + 1800

y = 2220

8 – Para receber R$ 2000,00 de salário em um mês, quantos produtos ele deve vender?

a) 20 produtos.

b) 25 produtos.

c) 23 produtos.

d) 15 produtos.

Resolução:

 y = 2000

y = 10x + 1800

2000 = 10x + 1800

2000 – 1800 = 10x

200 = 10x

x = 20

9 – Dada a função definida por f(x) = 2x + 3, determine f(1) , f(2) , f(3) e f(4).

a) { 5, 7, 9, 11}
b) { 7, 6, 10, 5}
c) { -5, 9, 11, -7}

d) ( 15, 9 , 7, 5}

Resolução:

f(x) = 2x + 3
f(1) = 2⋅1 + 3 = 2 + 3 = 5
f(2) = 2⋅2 + 3 = 4 + 3 = 7
f(3) = 2⋅3 +3 = 6 + 3 = 9
f(4) = 2⋅4 +3 = 8 + 3 = 11

Resposta: Letra A

10 – Dada a função de 1º grau y = 0,90x + 2,50, calcule o valor de x para y = 80.

Resolução:

y = 80
y = 0,90x + 2,50  ⇒  80 = 0,90x + 2,50
80 - 2,50 = 0,90x  ⇒  77,50 = 0,90x

x  =  86,1111111...

Exercícios com racionalização de denominadores

Racionalizar o denominador de uma fração cujo denominador é um radical com com raiz não exata, multiplicamos o numerador e o denominador dessa fração por um certo radical, de modo a tornar a fração com denominador racional.

Exercícios:

3 - Usando as propriedades de radicais, simplifique a expressão:

Resolução:

Veja:

4 - Simplifique a fração 

Resolução:

Para racionalizar o denominador da fração, vamos multiplicar o numerador e o denominador da fração por:

Pois:

Veja:

5 - A expressão abaixo é equivalente a:

Resolução:

Valor numérico de uma expressão algébrica

Para calcular o valor numérico de uma expressão algébrica, substituímos os valores das  variáveis/incógnitas na expressão algébrica e efetuamos as operações indicadas.

Para obter o valor numérico de uma expressão algébrica você deve proceder do seguinte modo:

1º) Substituir as letras por números reais dados.

2º) Efetuar as operações indicadas, devendo obedecer à seguinte ordem:

 a) potenciação e radiciação;

b) divisão e multiplicação;

c) adição e subtração.

Observação: Convém utilizar parênteses quando substituir na expressão algébrica números negativos.

Exemplos:

1 – Qual é o valor numérico da expressão algébrica 3x – 2y, para x = 4 e y = – 3?

 3・4 – 2・(– 3) = 12 + 6 = 18

 2 – Dada a expressão algébrica 2ab³. Se a = 7 e b = 4, o seu valor numérico será:

 2・7・4³ = 2・7・4・4・4 = 14・16・4 = 896

Exercícios

1 – Sabendo que x = 5, determine o valor numérico da expressão x + 1. 

a) 7

b) 6

c) 4

d) 5

 Resposta: 5 + 1 = 6

2 – Sabendo que x = 2 e y = 3 e calculando o valor numérico da expressão

4x² + 5y, termos:

 a) 31

b) 32

c) 33

d) 30

 Resposta: 4・2² + 5・3 = 4・2・2 + 15 =  4・4 + 15 = 16 + 15 = 31

3 – Sabendo que x = – 1, determine o valor numérico da expressão x + 1 – x². 

a) 1

b) 2

c) – 2

d) –1

 Resposta: (– 1) + 1 – (– 1)² = – 1 + 1 – (– 1)・(– 1) = – 1 + 1 – (+ 1) = 0 – 1 = – 1 

4 – Calculando o valor numérico da expressão abaixo para a = – 1 e p = 3

 

Vamos ter:

a) 1/2

b) 2

c) 1/3

d) – 2