1 - Calcule o 5º termo da PG (1, 5, ...).
b) 1 584
c) 2 225
d) 3 625
a) 81 b) 729 c) 243 d) 27
6 – Determinar o sétimo termo da PG: 3, 9, 27, ...
7 - Em uma PG, o primeiro termo é 4 e o quarto termo é 4000. Qual é razão dessa PG?
8 - Inserir dois meios geométricos reais entre – 3 e 24.
a) – 6
b) 6
c) 7
d) 5,5
e) 0
10 - Determine a razão q da PG na qual o 2º termo vale 12 e o 5º termo vale 324.
11 - Numa P. G. crescente, o quinto termo é 810 e o terceiro termo é 90. Calcule sua razão e o primeiro termo dessa progressão geométrica.
12 - Considere a PG: 2, 6, 18, 54, ... Encontre o seu 10º termo.
13 – Determinar o número de termos das seguintes progressões geométricas:
14 - Determinar o primeiro termo de cada progressão geométrica, dados:
15 – Calcule três números em PG crescente, de tal forma que a sua soma é 7 e o produto é 8.
16 – Calcule três números em PG crescente, de tal forma que a sua soma é 13 e o produto é 27.
17 – Numa PG, a1 = 2 e a6 = 486. Calcule a razão dessa PG.
18 – Calcule o 6º termo da PG (6, 12, ...).
19 - Numa PG, a1
= 3 e a8 = 384. Calcule a razão dessa PG.
1) Resolução:







3) Resolução:
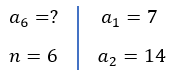






Cálculo da razão:



6) Resolução:
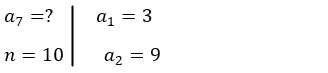
Cálculo da razão:

Fazendo n = 7:

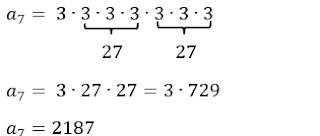


8) Resolução:
(– 3, __ , __ , 24)



Calculo do segundo termo:

Calculo do terceiro termo:

Resposta: (– 3, 6, – 12, 24)
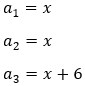
Cálculo da razão:






11) Resolução:

Fazendo n = 3:

Fazendo n = 5:

Dividindo (2) por (1):

q = 3 (P.G. crescente)
Cálculo do primeiro termo:

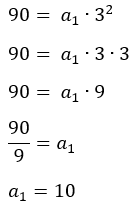
Resposta: A razão é 3 e o seu primeiro termo é 10.
12) Resolução:



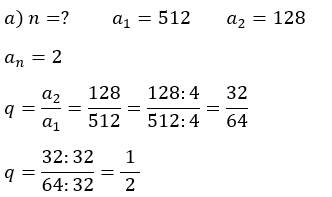



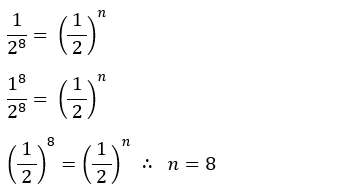
Resposta: essa progressão geométrica tem 8 termos.


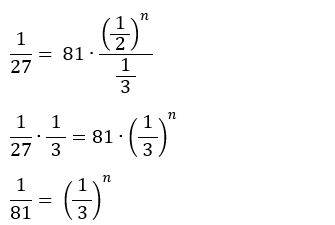
![]() Fatorando
81:
Fatorando
81:


Resposta: essa progressão geométrica tem 4 termos.

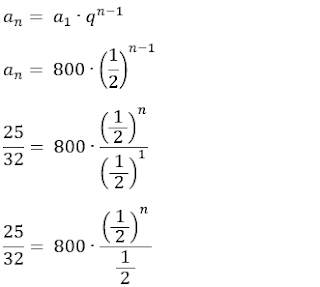


Fatorando 32 e 64:


Resposta: essa progressão geométrica tem 11 termos.
14) Resolução:

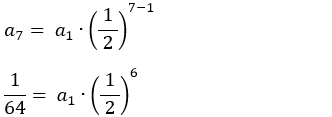





Fazendo n = 7:
Dividindo (2) por (1):




Para:

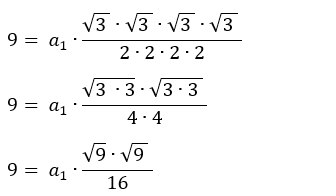
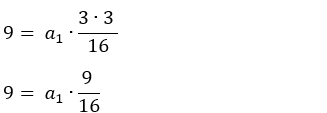

15) Resolução:



Multiplicando (3) por q:

Usando a fórmula de Bhaskara para calcular o valor de q:
a = 2, b = – 5 e c = 2


Para q = 1 e x = 2:
Como a PG é crescente:
Resposta:(1, 2, 4)
16) Resolução:


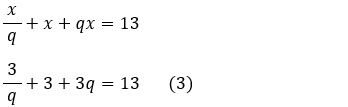
Multiplicando (3) por q:

Usando a fórmula de Bhaskara para calcular o valor de q:
a = 3, b = –
10 e c = 3

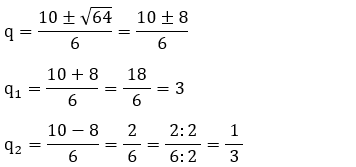
Para q = 1/3 e x = 3:
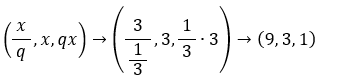

Como a PG é crescente:
Resposta: (1, 3, 9)
17) Resolução:
Dados:
= 2
n = 6


18) Resolução:

Cálculo da razão:
Cálculo de a6:

19) Resolução:


Fatorando o número 128:


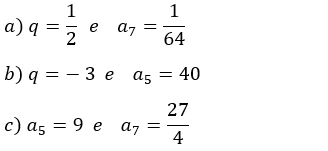
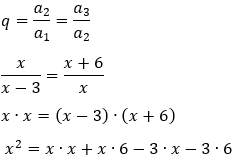
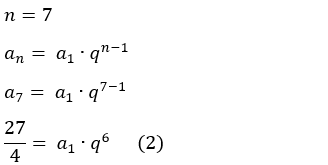
Nenhum comentário:
Postar um comentário