Para uma PG infinita, a soma dos termos só é possível se a razão (q) estiver entre – 1 e 1 (ou seja, – 1 < q < 1). Isso porque, se a razão for maior ou igual a 1 ou menor ou igual a – 1, a soma dos termos diverge (vai para infinito).
A fórmula para a soma de uma PG infinita é:

Onde:
a1 é o primeiro termo da PG.
q é a razão da PG.
Exemplos
1 – Calcular a soma da PG infinita:




2 - Considere a PG infinita: 1, 0.5, 0.25, 0.125, ...


Exercícios
1 - Calcular a soma da PG infinita:
![]()
2 - Resolva a equação:
![]()
4 – Determine a soma dos termos da PG infinita

5 – Determinar o valor de x na equação:
6 – Determinar a fração geratriz da dízima periódica 0,1212 ...
8 – Determinar a fração geratriz da dízima periódica 2,34444...
Respostas:
1) Resolução:
2) Resolução:
• Como S = 20:
S = 2x
3) Resolução:
4,322... = 4,3 + 0,02 + 0,002 + 0,0002 + ....
• A parte dessa soma: 0,02 + 0,002 + 0,0002 + .... é uma PG infinita.
Sendo:
• Substituindo esses valores na fórmula da soma:
• Substituindo o valor de “S”:
• Logo:
4) Resolução:
5) Resolução:
• Cálculo da razão q:
• Substituindo esses valores na fórmula:
• Como S = 20:
6) Resolução:
0,1212 ... = 0,12 + 0, 0012 + ...

• Calculo
da razão q:



7) Resolução:

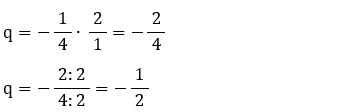


8) Resolução:
2,3444...= 2,3 + 0,04 + 0,004 + 0,0004 + ....
A parte dessa soma: 0,04 + 0,004 + 0,0004 + .... é uma PG infinita.
Dados:


Substituindo o valor de
“S”:
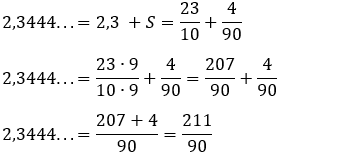
Logo:









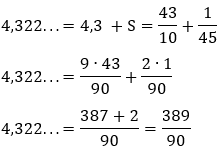










Nenhum comentário:
Postar um comentário