Exercícios com fatoração de polinômios

Fatorar um polinômio significa escrevê-lo na forma de produto (ou potência). As fatorações mais conhecidas são: fator comum em evidência, agrupamento, diferença entre dois quadrados, trinômio quadrado perfeito e diferença de dois cubos. 

• Fator Comum em Evidência

Usamos esse tipo de fatoração quando existir um fator que se repete em cada termo de um polinômio.

Veja os exemplos:

     Termo em evidência

     Termo em evidência

              Termo em evidência

• Agrupamento 

Agrupamento é o método pelo qual simplificamos expressões algébricas, colocamos os fatores comuns dos agrupamentos em evidência duas ou mais vezes. 

a) ax + 2bx + ay + 2by = x⋅(a + 2b) + y⋅(a + 2b) 

= (a + 2b)(x + y) 

b) 3ax + 6a + b²x + 2b² = 3a⋅(x + 2) + b²⋅(x + 2) 

= (x + 2)⋅(3a + b²)

• Trinômio Quadrado Perfeito 

O quadrado perfeito (a + b)² ou (a – b)² é composto por dois fatores (a e b). 

Assim, a fatoração do trinômio quadrado perfeito será: 

a² + 2ab + b² = (a + b)² 

a² – 2ab + b² = (a – b)² 

Exemplos: 

a) x² + 2xy + y² = (x + y)² 

b) x² – 2xy + y² = (x – y)² 

c) 9x² + 24xy + 16y² = (3x)² + 2·3x·4y + 16y² = (3x + 4y)² 

• Diferença de Dois Quadrados 

Para fatorar polinômios do tipo a² – b² usamos o produto notável da soma pela diferença. 
Assim, a fatoração de polinômios desse tipo será:

a² – b² = (a + b)(a – b)

Exemplos:

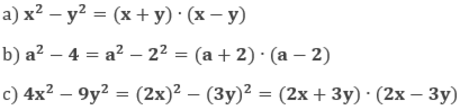
• Trinômio não Quadrado Perfeito

Exemplos: 

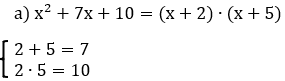
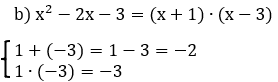
• Diferença de dois cubos

Exemplos: 

• Soma de dois cubos

Exemplos: 

Exercícios

1 – Sabendo que os trinômios a seguir são quadrados perfeitos, escreva a forma
fatorada de cada um deles.
a) 4x² – 12xy + 9y²
b) y² + 22y + 121

Resolução:

2 – Fatore o polinômio 4x² – y².

 Resolução:

4x² – y²  = (2x)² – y²

= (2x – y)⋅(2x + y) 

3 – Fatore o polinômio x³ + 3x² – 6x – 18.

 Resolução:

 x³ + 3x² – 6x – 18
= x²⋅(x + 3) – 6⋅(x + 3) 
= (x + 3)⋅( x² – 6)

4 – Fatore completamente o polinômio 3a²x – 3b²x + 2a² – 2b².

 Resolução:

3a²x – 3b²x + 2a² – 2b²

= 3x⋅(a² – b²) + 2⋅(a² – b²)

= (a² – b²)⋅(3x + 2)

= (a + b)⋅(a – b)⋅(3x + 2)

5 – Fatore o binômio x³ – 36x.

Resolução:

x³ – 36x = x⋅(x² – 36)

x³ – 36x = x⋅(x² – 6²) 

x³ – 36x = x⋅(x + 6)⋅(x – 6)

6 – Simplifique a expressão abaixo:

(2x + y)² + (2x – y)² + 2(2x – y)(2x + y)

• Resolvendo separadamente:

• Então:

7 – Usando fatoração, calcule o valor da expressão:

Resolução:

8 – Fatore o trinômio 2x² + 5x – 12.

Resolução:

2x² + 5x – 12

• Escrevendo 5x como 8x – 3x:

2x² + 5x – 12

= 2x² + 8x – 3x – 12

= 2x⋅x + 2x⋅4 – 3x – 3⋅4

= 2x⋅(x + 4) – 3⋅(x + 4)

= (x + 4)⋅(2x – 3)

9 – Fatore o binômio x⁶ – y⁶.

Resolução:

• Escrevendo x⁶ – y⁶ em forma de uma diferença de dois cubos:

x⁶ – y⁶ = (x²)³ – (y²)³

• Usando a fatoração da diferença de dois cubos:

a³ – b³    = (a – b)⋅(a² + a⋅b + b²)      

e

• Diferença de Dois Quadrados: 
a² – b² = (a + b)⋅(a – b)

• Vamos ter:

x⁶ – y⁶ = (x²)³ – (y²)³

= [x² – y²]⋅[(x²)² + x²⋅y² + (y²)²]

= (x + y)⋅(x - y)⋅(x⁴ + x²y² + y⁴)

10 – Fatore o trinômio 3x² + 7x – 6.

Resolução:

• Fazendo 3x = y:

• Logo: 3x² + 7x – 6 = (x + 3)⋅(3x – 2)

11 – Resolva a equação (n³)² = (2²)³.

Resolução:

(n³)² = (2²)³

(n³)² – (2³)² = 0

• Usando a fatoração de polinômios:

(n³)² – (2³)² = 0

(n³ + 2³).( n³ – 2³) = 0

• Usando as fatorações de polinômios:

e

(n³ + 2³)⋅( n³ – 2³) = 0

(n + 2)⋅(n² – n⋅2 + 2²)⋅(n – 2)⋅( n² + n⋅2 + 2²) = 0

(n + 2)⋅(n² – 2n + 4)⋅(n – 2)⋅( n² + 2n + 4) = 0

• Resolvendo a equação n² – 2n + 4 = 0:

• Resolvendo a equação n² + 2n + 4 = 0:

• Solução: