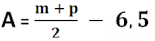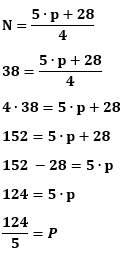Pontos no plano cartesiano

Exercícios resolvidos

1 – Complete os pares ordenados, com as coordenadas cartesianas dos pontos marcados, no desenho:

                       A(     ,     ), B(     ,     ), C(     ,     ), D(     ,     ) e E(     ,     )

Resposta:

A( 2 , 3 ), B( – 3 , 4 ), C(  3 , 2 ), D( – 4 , – 1 ) e E( 2 , – 3 )

2 – Localize no plano  cartesiano abaixo os pontos de coordenadas A( 2 , 3 ), 
B( – 2 , 3 ), C( 1 , – 2 ),  D( – 4 , – 2 ) e E( 3 , 0 ).

Resolução:

3 – No plano cartesiano da figura, localize os pontos A (2,3), B(–1, –2), C(–2,4), D(3,1), E(2, –3), 

F(2, – 2) e G(–1,0).

Resolução:

Exercícios com ângulos suplementares

1 – Dois ângulos são suplementares. Se um deles tem medida de 20º, qual a medida do outro? 

x + 20º = 180º

x = 180º – 20º

x = 160º

2 – Vamos calcular o valor de x nas figuras abaixo:

a) 

3x + 10º + 50º = 180º

3x + 60º = 180º

3x = 180º –  60º

3x = 120º

x = 120º/3

x = 40º

b) 

x + 90º + 2x = 180º

x + 2x = 180º – 90º

x + 2x = 180º – 90º

3x = 90º

x = 90º/3

x = 30º

       


c) 

2x + 20º + 2x = 180º

2x + 2x = 180º – 20º

4x = 160º

x = 160º/4

x = 40º

Exercícios com soma dos ângulos internos de um triângulo

2 – Calcule a medida do ângulo C no triângulo abaixo.

A + B + C = 180^o

68^o + 90^o + C = 180^o

C = 180^o  – 68^o – 90^o 

C = 22^o

3 – O desenho da figura abaixo é um triângulo isósceles.

     


      a)    Qual é o seu perímetro?

Perímetro é a soma dos lados:

P = 10 cm + 10 cm + 6 cm

P = 26 cm

      b)   Calcule a medida do 

            ângulo A.

A + B + C = 180^o

A + 65^o + 65^o = 180^o

A + 130^o = 180^o

A = 180^o – 130^o

A = 50^o

Exercícios com ângulos complementares

Ângulos complementares são dois ângulos cuja soma é igual a 90 graus. Em outras palavras, se você somar as medidas de dois ângulos complementares, o resultado será sempre 90°.

Exercícios

1 – Calcular o valor de x na figura abaixo, sabendo que os dois ângulos somam 90º.

Resolução:

2 – Calcular o valor de x na figura abaixo, sabendo que os três ângulos somam 90º.

Resolução:

X = 12°

Resposta: Letra B

3 – Calcular os valores dos quatro ângulos na figura.

Resolução:

Cálculos dos ângulos:

Resposta: Os ângulos medem 10°, 15°, 30° e 35°.

4 – Os ângulos das figuras abaixo são complementares. Calcule o valor de cada ângulo indicado:

Resolução:

a)

Resposta: 65° e 25°

Resposta: 60° e 30°

Figuras de fractais

Atividades desenvolvidas por alunos, na Mostra Cultural da Escola Madre Francisca - outubro/2018.

Fórmula de Tanner

 O pediatra britânico James Mourilyan Tanner, mundialmente conhecido pelas suas pesquisas sobre o crescimento normal e patológico e pela escala de avaliação do desenvolvimento puberal. Criou nos anos 1960 uma fórmula para estimar até que altura uma criança vai crescer, tomando como parâmetros a altura dos pais. Essa fórmula, que recebeu o nome de seu criador, Fórmula de Tanner, varia para o cálculo da altura de meninos em relação ao cálculo da altura de meninas. A fórmula Tanner  faz uma projeção, mas a principal influência para determinar a altura das crianças é  a hereditariedade. Existe, nesse cálculo, uma margem de erro de mais ou menos de 10% para cima ou para baixo.

👨 Para meninos:

👩 Para meninas:

 

Considere em centímetros:

A: altura da criança

M: altura da mãe

P: altura do pai

Exemplo: De acordo com a fórmula, sabendo que um pai tem 1,72 m (172 cm) e uma  mãe tem 1,50 m (150 cm):

a)   Até que altura estima-se que um menino, filho do casal, vai crescer?

Para menino, vamos usar a fórmula:

A = 167,5 cm

ou aproximadamente

A = 1,68 m

b) Até que altura estima-se que uma menina, filha do casal, vai crescer?

Para menina, vamos usar a fórmula:

A = 154,5 cm

ou aproximadamente

A = 1,55 m

Unidade de medida de calçado

Com a unidade de medida de calçado padronizada é possível que uma relação entre o número do calçado (N) e o comprimento do pé (p), em centímetros.

No Brasil, por exemplo, podemos estabelecer essa relação por meio de uma fórmula:

Exemplos:
1 - Utilizando essa fórmula, vamos determinar o número do calçado para uma criança cujo comprimento do pé é de 22 cm. 

Fazendo p = 22 cm, vamos ter:

Ou seja, o número do calçado dessa criança deverá ser 28.

 2- Qual é o comprimento do pé de uma pessoa que usa uma calçado de número 38?

 Fazendo N = 38, vamos ter:

p = 24,8 cm