Funcionamento de um termômetro

Posted: 14 Dec 2016 06:10 AM PST Já foi falado no infoEnem sobre temperatura (clique aqui e veja o artigo) e também sobre escalas termométricas. Assim sendo, podemos entender o funcionamento de um dos instrumentos mais importantes no estudo da física e da química: o termômetro. Entretanto, antes de entrarmos no funcionamento do termômetro propriamente dito, temos que entender o que são substâncias termométricas e grandezas termométricas. Vamos lá: Substâncias termométricas – são aquelas que uma (ou mais!) de suas propriedades físicas se alteram, de maneira mensurável, com a temperatura. Grandeza termométrica: é a propriedade da substância termométrica que se altera com a temperatura. Um ótimo exemplo é o mercúrio, que é considerado uma substância termométrica, já que o seu volume varia de acordo com a temperatura. Neste caso, o volume é a grandeza termométrica do mercúrio. Fácil, não é? E será justamente o mercúrio nossa “peça chave” para entender o funcionamento de um termômetro. Veja abaixo o esquema que mostra a construção de um termômetro de mercúrio: Na extremidade da esquerda, há um pequeno reservatório (chamado bulbo), onde temos nossa maior quantidade da nossa substância termométrica (Hg). Já no interior da haste (tubo de vidro), temos um tubo muito estreito.(capilar), no qual o mercúrio se desloca da seguinte maneira: Quando a temperatura aumenta, o mercúrio se expande e, consequentemente, a coluna de mercúrio se desloca para a direita. De forma análoga, mas contrária, quando a temperatura diminui, o mercúrio se contrai e, consequentemente, a coluna de mercúrio se desloca para a esquerda. Pronto, nosso termômetro está quase pronto, basta apenas escolher uma escala termométrica (clique aqui para relembrar o conteúdo sobre escalas termométricas) e calibrar o instrumento, utilizando dois pontos fixos e que não dependam da nossa sensação térmica (que, como já vimos, é enganosa). Os pontos fixos mais utilizados são os pontos de fusão e de ebulição da água, pois são situações fáceis de reproduzir em qualquer local e/ou laboratório. Claro que hoje em dia existem muitos termômetros, como o de gás e o digital, estes bem mais modernos e precisos. Entretanto, suas construções, de uma forma ou de outra, acabam relacionando a variação de alguma grandeza termométrica de alguma substância com a calibração do instrumento conforme a escala termométrica escolhida. O post Entenda tudo sobre o Funcionamento de um Termômetro apareceu primeiro no infoEnem.

A diferença entre fissão nuclear e fusão nuclear

Posted: 05 Feb 2017 10:28 AM PST Com a desenvolvimento da ciência e principalmente dos estudos da física quântica, o homem começou a entender e manipular, como nunca antes na história, a energia nuclear. Em outras palavras, começamos a aproveitar parte do gigantesco potencial energético dos processos de transformação de núcleos atômicos. Tanto para o bem quanto para o mal. Neste artigo, veremos as diferenças teóricas entre a fissão e a fusão nuclear, além é claro de exemplos de aplicações e curiosidades de cada uma delas. Vamos lá! Fissão nuclear A fissão nuclear é a “quebra” , ou divisão, de um átomo mais pesado em outros, evidentemente mais leves que o original. Na prática, esse processo ocorre com o bombardeamento de nêutrons em núcleos radioativos, gerando isotopos instáveis que, por sua vez, culmina com as rupturas desses núcleos, gerando uma reação em cadeia (pois outros nêutrons atingirão outros núcleos) e liberando uma grande quantidade de energia. Temos diversos exemplos da utilização da fissão nuclear. Certamente, os mais conhecidos são a produção de energia elétrica, através da fissão do urânio, e a fabricação de bombas atômicas, como as que devastaram as cidades de Hiroshima e Nagasaki em 1945. Vale ressaltar que, a grosso modo, a diferença entre o reator de uma usina nuclear e a bomba atômica é que, no primeiro caso, a reação em cadeia é controlada. Nas bombas atômicas, não. Fusão nuclear Ao contrário da fissão, a fusão nuclear acontece quando dois elementos se chocam para formar um novo elemento, evidentemente mais pesado. A liberação de energia na fusão nuclear é muito superior que na fissão. O melhor exemplo de um processo de fusão nuclear é o Sol. Isso mesmo! Toda a energia que recebemos do “Astro Rei” vem da fusão de átomos de hidrogênio, que se chocam e geram átomos de hélio. Quanto a aplicação da fusão nuclear pelo homem, temos a bomba de hidrogênio, criada em 1952. Para se ter uma ideia, essa surpreendente arma de destruição gerou, apenas no seu teste inicial, uma liberação de energia mil vezes maior do que as bombas atômicas que destruíram as cidades japonesas no final da segunda guerra mundial. Entretanto, por necessitar de elevadíssimas temperaturas e condições especiais de pressão para acontecer, a utilização da energia de fusão nuclear para gerar energia elétrica ainda não apresenta viabilidade econômica. Fica a torcida para que em breve consigamos aplicar tais conhecimentos. Afinal, ao contrário da fissão nuclear, a fusão não apresentaria lixo radioativo. Isso porque, provavelmente, seria utilizada a fusão de átomos de hidrogênio, que resultaria na liberação de gás hélio (inerte e não-radioativo), sendo assim considerada uma produção de energia “limpa”. O post Conheça as diferenças entre fissão e fusão nuclear apareceu primeiro no infoEnem.

Média Aritmética Simples

A média aritmética é o resultado da divisão entre a soma de vários valores pela quantidade de valores somados.

Podemos calcular a média aritmética usando a expressão:

Exemplos:

1 - Qual é a média aritmética simples dos números 12, 8 e 13?
a) 9
b) 10,4
c) 11
d) 9,3

Resolução:

2 - Os jogadores de uma equipe de basquete apresentam as seguintes idades: 28, 29, 19, 23 e 21 anos. Qual a média de idade desta equipe?

Resolução:

   

Resposta: A média de idade desta equipe é de 24 anos.

3 - Em um grupo de seis amigos, foram computadas suas idades. Determine qual a idade média desse grupo.

Nomes	Idades (anos)
Paulo	12
Carlos	13
André	15
Roberto	17
José	19
Pedro	20

Resolução:

Resposta: A média de idade desse grupo é de 16 anos.

4 - João deseja calcular a média aritmética das notas que tirou em matemática. Calcule a média de suas notas em matemática.

Matemática
1ª prova	8,6
2ª prova	9,3
3ª prova	9,7
4ª prova	10,0

• a) 9,4
• b) 8,9
• c) 9,3
• d) 9,8

Resolução:

5 - (PUC-RIO) – As notas de uma turma de alunos no teste de matemática foram 10, 10, 9, 8, 8, 8, 7, 7, 4 e 2. Qual a média da turma?

a) 7,8

• b) 8,2
• c) 7,3
• d) 8,0

Resolução:

6 - O dólar é considerado uma moeda de troca internacional, por isso, o seu valor diário possui variações. Acompanhando a variação de preços do dólar em reais durante uma semana, foram verificadas estas variações:

Segunda feira	Terça feira	Quarta feira	Quinta feira	Sexta feira
R$ 5,20	R$ 5,40	R$ 5,30	R$ 5,50	R$ 5,80

Determine o valor médio do preço do dólar nessa semana.

a) R$ 5,66
b) R$ 5,44
c) R$ 5,34
d) R$ 5,52

Resolução:

7 - A média aritmética entre dois números é 50 e um dos números e 35 qual é o outro número?

Resolução:

Resposta: o outro número é 65.

8 - (AGENTE-ADM) A média aritmética das idades de 10 alunos de uma determinada turma é igual a 15 anos. Se dois alunos, um com 12 anos e o outro com 18 anos, saírem dessa turma, a media aritmética das idades dos 8 alunos restantes será igual a:

a) 13 anos

b) 14 anos

c) 15 anos

d) 16 anos

Resolução:

Média aritmética das idades de 10 alunos:

Média aritmética das idades de 8 alunos:

9 - Uma escola tem 18 professores. Um deles se aposenta e é substituído por um de 22 anos. Com isso, a média das idades dos professores diminui 2 anos. A idade em anos do professor que se aposentou é:

a) 52           b) 54           c) 56            d) 58

Resolução:

Média antes da aposentadoria:

Média depois da aposentadoria:

Comparando (1) e (2):

Luz

Posted: 27 Jun 2016 08:52 AM PDT O segmento da Física que estuda a luz é a óptica. A palavra óptica vem do grego optiké e significa relativa à visão. Na Antiguidade clássica, os filósofos gregos como Platão (428 ou 427 - 347 a.C.) e Aristóteles (384 - 322 a.C.) já perguntavam: o que é a luz? Por que vemos um objeto? Nessa época, por exemplo, acreditava-se que os olhos emitiam partículas que tornavam os objetos visíveis - hoje se sabe que só conseguimos enxergar objetos se a luz for refletida ou emitida por eles. Primeiro, a resposta: A luz é uma onda eletromagnética. Sendo um pouco mais técnico, podemos dizer que é um fenômeno ondulatório onde um campo magnético e um elétrico se alimentam e que se propaga no vácuo e em diversos meios (como aguá e ar). No vácuo, a velocidade de propagação é de quase 300 mil quilômetros por segundo! Abaixo segue uma esquematização de uma onda eletromagnética. Note que essa onda é considerada transversal, pois tanto a campo magnético quanto o elétrico têm oscilações perpendiculares à propagação. Entretanto, além do caráter ondulatório, temos aí um ingrediente a mais: a luz também apresenta partículas de massa zero, conhecidas atualmente como fótons. Tal característica foi defendida arduamente por ninguém mais que Isaac Newton no início do século XVIII e, posteriormente, comprovada (através do efeito fotoelétrico) por um cientista não menos importante, Albert Einstein. Essa dualidade da luz, que apresenta ao mesmo tempo de características ondulatórias e corpusculares (de partícula), além da dificuldade de medição de diversos fenômenos, fez com que cientistas de todo o mundo a estudassem literalmente “esquecendo” algumas de suas propriedades. Por exemplo: Óptica Geométrica: É o estudo da luz desprezando seu caráter ondulatório e corpuscular. Nessa área, são considerados apenas os fenômenos ópticos resultantes da propagação retilínea da luz, amplamente aplicada para a construção de lentes e espelhos. Eletromagnetismos: Aqui, é estudado todo o caráter ondulatório da luz, deixando de lado sua face corpuscular. Pensa que acabou? A luz também é fundamental em diversos ramos da física moderna, como na teoria da relatividade, de Einstein, e na mecânica quântica, que estuda as interações subatômicas. E caso ache que não seja importante estudar e conhecer essas diversas caraterísticas da Luz, clique aqui e veja um exemplo de questão do Enem que cobrava justamente o entendimento do seu caráter ondulatório. O post Física para o Enem: Afinal, o Que É a Luz? apareceu primeiro no infoEnem.

Força Elétrica - Lei de Coulomb

A força elétrica é uma das forças fundamentais da natureza e desempenha um papel crucial na física e em diversas aplicações tecnológicas. Ela está associada às interações entre partículas carregadas eletricamente, como prótons e elétrons.

Essa força é descrita pela Lei de Coulomb, que afirma que a intensidade da força entre duas cargas é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas. A expressão matemática é:

Onde: F é a força elétrica, medida em newton (N); k é a constante eletrostática, medida em (N⋅m2/C2); q1 e q2 são as cargas, medidas em coulomb (C); r é a distância entre elas, medida em metros (m). A constante eletrostática do meio (k) depende da permissividade elétrica do meio (ε ), ou seja, é a maneira como o campo elétrico interage com o meio físico em que os corpos se encontram. A relação entre a constante eletrostática do meio (k) e a permissividade elétrica do meio ( ε ) é descrita na seguinte equação: Quando estamos trabalhando com o vácuo utilizamos ε0 (permissividade elétrica no vácuo), nesse caso, ε0 vale 8,85 x 10-­12C2/N⋅m2, e portanto, utilizando a equação descrita anteriormente k0 vale 9 x 109 N⋅m2/C2. Relação entre força elétrica e campo elétrico O Campo Elétrico (E) é definido como a força elétrica por unidade de carga. Em termos matemáticos, é expresso como E = F/q, onde F é a força sobre uma carga de teste q. A força elétrica pode ser atrativa (quando as cargas têm sinais opostos) ou repulsiva (quando as cargas têm o mesmo sinal). Essa interação é fundamental para explicar fenômenos como a formação de átomos, moléculas e os comportamentos de materiais em diferentes contextos:    Atração     Repulsão Repulsão EXEMPLOS 1 - (Unifesp) Duas partículas de cargas elétricas Q = 4,0⋅10−16 C e q = 6,0⋅10−16 C estão separadas no vácuo por uma distância de 3,0⋅10−9 m. Sendo ko = 9 ⋅109 N⋅m2 / C2, a intensidade da força de interação entre elas, em newtons, é de: A) 1,2⋅10−5 N B) 1,8⋅10−4 N C) 2,0⋅10−4 N D) 2,4⋅10−4 N E) 3,0⋅10−3 N Resolução:  Q = 4,0⋅10−16 C  q = 6,0⋅10−16 C  r = 3,0⋅10−9 m k0 = 9⋅109 N⋅m2 / C2  F = 2,4⋅10−4 N 2 - (Mack-SP) Uma carga elétrica puntiforme com q = 4,0 μC, que é colocada em um ponto P do vácuo, fica sujeita a uma força elétrica de intensidade 1,2 N. O campo elétrico nesse ponto P tem intensidade:  a) 3,0∙105 N/C b) 2,4∙105 N/C c) 1,2∙105 N/C d) 4,0∙10−6 N/C e) 4,8∙10−6 N/C Resolução:  E = ? F = 1,2 N q = 4,0 μC = 4,0⋅10 – 6 C 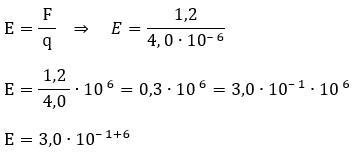  E = 3,0∙105 N/C       EXERCÍCIOS  1 - Duas cargas puntiformes de valores Q1 = 5μC e  Q2 = − 10μC estão a uma distância de 5 cm. Qual é a força elétrica entre elas? Determine também se ela é repulsiva ou atrativa. A) 180 N, atrativa. B) 100 N, repulsiva. C) 180 N, repulsiva. D) 1000 N, atrativa. E) 1,8 N, atrativa. Resolução: Q1 = 5μC = 5⋅10 – 6 C Q2 = − 10μC = − 10⋅10 – 6 C k = 9⋅109 N⋅m2 / C2 r = 5 cm = 5:100 m = 0,05 m = 5⋅10 – 2 m F = ?  F = 180 N A força elétrica é atrativa, porque as cargas possuem sinais contrários. 2 - Uma carga elétrica com valor de 10 μC possui campo elétrico com valor de 3,0∙105 N/C. Determine a força elétrica gerada. A) 3,0 N B) 10∙103 N C) 3,0∙10−2 N D) 3,0∙10−3 N E) 3,0∙102 N Resolução:  E = 3,0∙105 N/C q = 10⋅10 – 6 C  F = ? F = 3 N 3 - Uma partícula possui campo elétrico com valor de 200∙105 N/C e força elétrica com valor de 5,0∙105 N. Determine o valor da carga elétrica. A) 0,025 C B) 0,05 C C) 0,055 C D) 0,045 C E) 0,035 C Resolução:  E = 200∙105 N/C F = 5,0∙105 N q = ? q = 0,025 C 4 - Uma carga q e outra Q, com o dobro de q, estavam inicialmente a uma distância d e foram reposicionadas a uma distância equivalente ao dobro da inicial. A força elétrica final será de quanto da força inicial? Resolução:  Força inicial: Força final: Multiplicando o numerador e o denominador da fração por 2: Logo: 5 - (UEL) Duas cargas iguais de 2⋅10−6 C se repelem no vácuo com uma força de 0,1 N. Sabendo-se que a constante elétrica do vácuo é 9⋅109 N⋅m2 / C2, a distância entre as cargas, em metros, é de: A) 0,9 B) 0,6 C) 0,5 D) 0,3 E) 0,1 Resolução:  q1 = q2 = 2⋅10 – 6 C F = 0,1N k = 9⋅109 N⋅m2 / C2 r = ? r = 0,6 m