Semelhança de triângulos

A semelhança de triângulos é um conceito fundamental da geometria que descreve quando dois triângulos possuem a mesma forma, independentemente de seu tamanho. Para que dois triângulos sejam semelhantes, seus ângulos correspondentes devem ser iguais e seus lados proporcionais.

Critérios de Semelhança:

Um triângulo pode ser semelhante a outro se satisfizer um dos seguintes critérios:

1. AA (Ângulo-Ângulo): Se dois ângulos de um triângulo forem iguais a dois ângulos de outro triângulo, então os triângulos são semelhantes.
2. LAL (Lado-Ângulo-Lado): Se dois lados de um triângulo forem proporcionais aos lados correspondentes de outro triângulo e o ângulo entre eles for igual, os triângulos são semelhantes.
3. LLL (Lado-Lado-Lado): Se os três lados de um triângulo forem proporcionais aos lados correspondentes de outro triângulo, então os triângulos são semelhantes.

Propriedades e Aplicações:

• A semelhança de triângulos é usada em trigonometria, topografia e desenho técnico.
• É útil para resolver problemas de proporcionalidade, como cálculo de alturas inacessíveis e distâncias em mapas.
• A Razão de Semelhança permite determinar dimensões desconhecidas em figuras geométricas

Exercícios 

1 - Determine a medida do lado x do quadrado AFDE da figura:

          

Resolução:

• Os triângulos ABC e BDF são semelhantes, então vale a relação:

• Multiplicando cruzado:

x = 1,2 m

2 - A medida de x no triângulo ABC é:

a) 2.           b) 3.           c) 4.           d) 5.

Resolução:

• Os triângulos ABC e A’B’C’ são semelhantes, então vale a relação:

• Multiplicando cruzado:

x = 5 cm

3 - (Aprendiz de Marinheiro - 2017) Observe a figura abaixo:

Um prédio projeta no solo uma sombra de 30 m de extensão no mesmo instante em que uma pessoa de 1,80 m projeta uma sombra de 2,0 m. Pode-se afirmar que a altura do prédio vale

a) 27 m
b) 30 m
c) 33 m
d) 36 m
e) 40 m

Resolução:

• Sendo os triângulos semelhantes, podemos escrever a seguinte proporção:

• Multiplicando cruzado:

x = 27 m

4 - (Fuvest - 2017) Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado  e N o ponto médio do lado . Os segmentos e  interceptam o segmento  nos pontos E e F, respectivamente.

• A área do triângulo AEF é igual a

Resolução:

• Os triângulos ABF e NCF são semelhantes:

• Multiplicando cruzado:

• Resolvendo o sistema de equações:

• Substituindo (1) em (2):

• Substituindo (3) em (1):

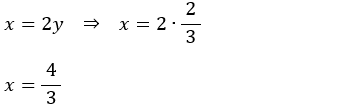
• O triângulo GBE é isósceles e triângulos AGE e ABM são semelhantes:

• Cálculo da área do triângulo ABF:

• Cálculo da área do triângulo ABE:

• Assim, a área do triângulo AEF será igual a:

5 - (Unirio) Numa cidade do interior, à noite, surgiu um objeto voador não identificado, em forma de disco, que estacionou a 50 m do solo, aproximadamente. Um helicóptero do exército, situado a aproximadamente 30 m acima do objeto, iluminou-o com um holofote, conforme mostra a figura anterior. 

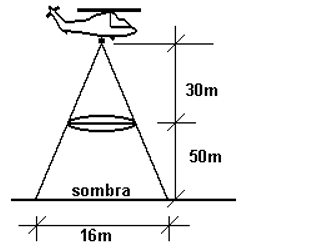
• Sendo assim, pode-se afirmar que o raio do disco-voador mede, em m, aproximadamente:

a) 3,0

b) 3,5

c) 4,0

d) 4,5

e) 5,0

Resolução:

• Multiplicando cruzado:

D = 6 m                             

• Como o diâmetro é o dobro do raio:

D = 2⋅r ⇒ 6 = 2⋅r

r = 3 m

6 - Sobre a congruência de triângulos, julgue as afirmativas a seguir:

I – Ao comparar dois triângulos, se a medida dos ângulos for congruente, então, podemos afirmar que esses triângulos são congruentes pelo caso Ângulo, Ângulo e Ângulo.

II – Dois triângulos equiláteros podem não ser congruentes.

III – Ao comparar dois triângulos, as medidas dos lados forem congruentes um a um, então, podemos afirmar que esses triângulos são congruentes.

Marque a alternativa correta:

A) Somente a I é verdadeira.

B) Somente a II é verdadeira.

C) Somente a III é verdadeira.

D) Somente a II é falsa.

E) Somente a I é falsa.

Resolução:

• I - É FALSO, pois ter apenas os ângulos congruentes implica que eles são semelhantes e não congruentes.

• II – É VERDADEIRO, pois podem ter lados com medidas diferentes e nesse caso serão semelhantes e não congruentes.

• III – É VERDADEIRO, pelo caso LLL da congruência de triângulos

Resposta: Letra E

7 - (Unicamp) Uma rampa de inclinação constante, como a que dá acesso ao Palácio do Planalto em Brasília, tem 4 metros de altura na sua parte mais alta. Uma pessoa, tendo começado a subi-la, nota que após caminhar 12,3 metros sobre a rampa está a 1,5 metros de altura em relação ao solo.

a) Faça uma figura ilustrativa da situação descrita.

b) Calcule quantos metros a pessoa ainda deve caminhar para atingir o ponto mais alto da rampa.

Resolução:

a)

b) 

• Multiplicando cruzado:

x = 20,5 m                              

8 - (Vunesp) Um obelisco de 12 m de altura projeta, num certo momento, uma sombra de 4,8 m de extensão. Calcule a distância máxima que uma pessoa de 1,80 m de altura poderá se afastar do centro da base do obelisco, ao longo da sombra, para, em pé, continuar totalmente na sombra.

Resolução:

• Cálculo da medida da sombra de uma pessoa de 1,8m:

• Multiplicando cruzado:

x = 0,72m                             

• Agora temos que tirar 0,72m de 4,8, para a pessoa, em pé, continue totalmente na sombra:

4,8 – 0,72 = 4,08 m

Resposta: A pessoa poderá se afastar do centro da base do obelisco 4,08 m, ao longo da sombra, para, em pé,  continuar totalmente na sombra.

9 - (Unesp) Uma gangorra é formada por uma haste rígida AB, apoiada sobre uma mureta de concreto no ponto C, como na figura. Quando a extremidade B da haste toca o chão, a altura da extremidade A em relação ao chão é:

Resolução:

• Cálculo da altura H₁:

• Usando o teorema de Pitágoras no triângulo CEG:

• Os triângulos CEG e ABF são semelhantes:

• Multiplicando cruzado:

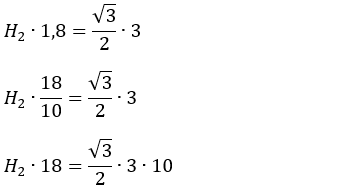
• Simplificando a fração:

Resposta: Letra D