A energia potencial elástica é a energia armazenada em um corpo elástico quando ele é deformado – esticado ou comprimido – e tem tendência a retornar à sua forma original. Esse conceito é fundamental na física e aparece em diversos contextos, como molas, elásticos e até mesmo músculos humanos.
Ela é determinada pela equação:
Onde:
- ( Epe
) é a energia potencial elástica (medida em Joule),
- ( k
) é a constante elástica do material (rigidez da mola) (medida em N/m),
- ( x
) é a deformação do corpo em relação à sua posição de equilíbrio (medida
em metros).
Conceitos Importantes:
- Lei de Hooke: Relaciona a força
aplicada a um objeto elástico com a deformação sofrida por ele, expressa
por:
F = k⋅x
- Armazenamento
e Liberação de Energia: Quando a força que causa a deformação é
removida, a energia potencial elástica pode ser transformada em energia
cinética.
- Aplicações:
Esse conceito é amplamente utilizado em engenharia mecânica, esportes
(como arcos e flechas), sistemas de suspensão de veículos e até em
brinquedos, como camas elásticas.
1 – (FUND. CARLOS CHAGAS) Uma mola elástica ideal, submetida
a ação de uma força de intensidade F = 10 N, está deformada em 2,0 cm. A
energia elástica armazenada na mola é de:
A) 0,10 J
B) 0,20 J
C) 0,50 J
D) 1,0 J
E) 2,0 J
Resolução:
x = 2 cm = 1:100 m = 0,02 m
F = 10 N
Cálculo
da constante elástica da mola (Lei de Hooke):
F = k⋅x ⇒ 10 = k⋅0,02
Cálculo da energia potencial elástica:

Epe = 0,1 J
Resposta: Letra A
2 – Calcule a deformação sofrida por um material elástico de
constante elástica 40 N/m que adquire uma energia potencial elástica de 3,2 J.
A) 0,2 m
B) 0,4 m
C) 0,6 m
D) 0,8 m
E) 1,0 m
Resolução:
Epe = 3,2 J
k = 40 N/m


x
= 0,4 m
Exercícios
1 – (FUND. CARLOS CHAGAS) Uma mola elástica ideal,
submetida a ação de uma força de intensidade F = 10N, está deformada de 2,0 cm.
A energia elástica armazenada na mola é de:
a) 0,10 J
b) 0,20 J
c) 0,50 J
d) 1,0 J
e) 2,0 J
Resolução:
Cálculo
da constante elástica da mola (Lei de Hooke):
F = 10 N
x = 2 cm = 2:100 m = 0,02 m
F = k⋅x
10 = k⋅0,02
K = 500 N/m
Calculo da energia potencial elástica:

Epe = 0,1 J
2 – (UEG) Em um experimento que valida a
conservação da energia mecânica, um objeto de 4,0 kg colide horizontalmente com
uma mola relaxada, de constante elástica de 100 N/m. Esse choque a comprime 1,6
cm. Qual é a velocidade, em m/s, desse objeto antes de se chocar com a mola?
A) 0,02
B) 0,40
C) 0,08
D) 0,13
Resolução:
m = 4,0 kg
k = 100 N/m
x = 1,6 cm = 1,6:100 m = 0,016 m
A energia cinética inicial do objeto é convertida em energia potencial elástica na mola:


Simplificando:


v = 0,08 m/s
Resposta: Letra C
3 – (UNESP - 2018 - 1ª FASE) Uma mini cama elástica é constituída por uma superfície elástica presa a um aro lateral por 32 molas idênticas, como mostra a figura. Quando uma pessoa salta sobre esta mini cama, transfere para ela uma quantidade de energia que é absorvida pela superfície elástica e pelas molas.

Considere que, ao saltar sobre uma dessas mini camas, uma
pessoa transfira para ela uma quantidade de energia igual a 160 J, que 45%
dessa energia seja distribuída igualmente entre as 32 molas e que cada uma
delas se distenda 3,0 mm. Nessa situação, a constante elástica de cada mola, em
N/m, vale
a) 5,0 × 105.
b) 1,6 × 101.
c) 3,2 × 103.
d) 5,0 × 103.
e) 3,2 × 100
Resolução:
Número de molas: 32
Energia absorvida 160 J
Energia absorvida apenas pelas molas:
45% de 160 J
Epe = 72 J
72 J distribuídos para 32 molas significa que cada mola
absorverá 2,25 J:
72 J:32 = 2,25 J
Distensão de cada mola:
x = 3,0 mm = 3:1 000 m = 0,003 m = 3⋅10
- 3 m
Cálculo da constante K de cada mola:


Isolando k, temos:

k = 5⋅105
N/m
4 – (Fatec) Um bloco de massa 0,60 kg é abandonado, a partir do
repouso, no ponto A de uma pista no plano vertical. O ponto A está a 2,0 m de
altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m.
São desprezíveis os efeitos do atrito e adota-se g = 10 m/s2. A
máxima compressão da mola vale, em metros:
B) 0,40
C) 0,20
D) 0,10
E) 0,05
Resolução:
m = 0,60 kg
k = 150 N/m
h = 2 m
x = ?
A energia potencial gravitacional se converte em energia
potencial elástica:
x = 0,4 m
5 – (ENEM – 2007)

Istoé, n.o 1.864, set./2005, p. 69 (com adaptações).
Com o projeto de mochila ilustrado acima, pretende-se aproveitar, na geração de energia elétrica para acionar dispositivos eletrônicos portáteis, parte da energia desperdiçada no ato de caminhar. As transformações de energia envolvidas na produção de eletricidade enquanto uma pessoa caminha com essa mochila podem ser assim esquematizadas:
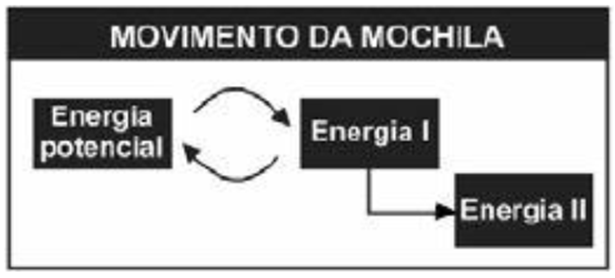
As energias I e II, representadas no esquema acima, podem ser identificadas, respectivamente, como
a) cinética e elétrica.
b) térmica e cinética.
c) térmica e elétrica.
d) sonora e térmica.
e) radiante e elétrica.
Resolução:
Alternativa (a): cinética e elétrica
6 – (ENEM – 2005) Observe a situação descrita na tirinha
abaixo.

Assim que o menino lança a flecha, há transformação de um tipo de energia em outra. A transformação, nesse caso, é de energia
a) potencial elástica em energia gravitacional.
b) gravitacional em energia potencial.
c) potencial elástica em energia cinética.
d) cinética em energia potencial elástica.
e) gravitacional em energia cinética.
Resolução:
Alternativa (c): potencial elástica em energia cinética.
7 - (Enem) Os carrinhos de brinquedo podem ser de vários
tipos. Dentre eles, há os movidos a corda, em que uma mola em seu interior é
comprimida quando a criança puxa o carrinho para trás. Ao ser solto, o carrinho
entra em movimento enquanto a mola volta à sua forma inicial. O processo de
conversão de energia que ocorre no carrinho descrito também é verificado em:
B) um freio de automóvel.
C) um motor a combustão.
D) uma usina hidroelétrica.
E) uma atiradeira (estilingue).
Resolução: