Lei de Stevin

A Lei de Stevin é um princípio fundamental da hidrostática que descreve a variação da pressão em um fluido em equilíbrio sob a influência da gravidade. Ela estabelece que a pressão em um ponto dentro de um líquido depende da profundidade e da densidade do fluido, sendo expressa pela equação:

p = p₀ + ρ⋅g⋅Δh   ou   Δp = ρ⋅g⋅Δh

Onde:

• ( p ) é a pressão em um ponto dentro do líquido,
• ( P₀ ) é a pressão na superfície do líquido (geralmente a pressão atmosférica),
• ( ρ ) é a densidade do fluido,
• ( g ) é a aceleração da gravidade,
• ( Δh ) é a profundidade do ponto abaixo da superfície do líquido,
• (Δp) é a variação da pressão.

Conceitos Importantes:

1. Pressão Hidrostática: A pressão aumenta à medida que a profundidade aumenta, devido ao peso da coluna de fluido acima do ponto analisado.
2. Independência da Forma do Recipiente: A pressão em um determinado nível depende apenas da profundidade e da densidade do fluido, não da forma do recipiente.
3. Aplicações: Esse princípio é essencial para engenharia hidráulica, cálculo de forças em barragens, mergulho submarino e até meteorologia, onde é usado para entender variações de pressão atmosférica.

Lembrando que:

m = µ ∙ V (sendo m = massa, µ = massa específica e V = volume)

A massa específica (µ) e a densidade (ρ) são grandezas físicas bem similares, já que ambas tratam a respeito da razão entre a massa e o volume. Contudo, enquanto a massa específica é a razão entre a massa da substância e o seu volume, a densidade é a razão entre a massa de um corpo e o seu volume.

A unidade de medida de pressão no sistema internacional é o N/m² (newton por metro quadrado), porém existem outros tipos de unidade de pressão, como atm (atmosfera), mmHg (milímetro de mercúrio), bar (bares), e pascal (Pa).

A relação entre as unidades de medida de pressão:

1 atm = 1,01325·10⁵ N/m² = 1,01325·10⁵ Pa = 760 mmHg = 1,01325 bar

Exemplos

1 - Qual a pressão em um ponto a 2 metros de profundidade em um lago, considerando a densidade da água como 1000 kg/m³ e a aceleração da gravidade como 10 m/s²? 

Resolução:

Aplicando a lei de Stevin:

Δp = ?

Δh = 2 m

g = 10 m/s²

𝜌 = 1000 kg/m³

Δp = 𝜌⋅𝑔⋅Δℎ

Δp = 1000⋅10⋅2

Δp = 20 000 Pa   ou   Δp = 20 kPa

2 - Um recipiente de 1,5 m está totalmente cheio de um líquido cuja densidade vale 1 200 kg/m³, e, no fundo dele, está uma moeda. Qual é o valor da pressão total sobre a moeda? Utilize a gravidade valendo 10 m/s².

Resolução

p₀ = 1,0⋅10⁵ N/m²

𝜌 = 1 200 kg/m³

g = 10 m/s²

Δh = 1,5 m

p = ?

p = p₀ + ρ⋅g⋅Δh

p = 1,0⋅10⁵ + 1 200⋅10⋅1,5

p = 1,0⋅10⁵ + 18 000

p = 1,0⋅10⁵ + 0,18⋅10⁵ 

p = 1,18⋅10⁵ N/m²

Exercícios

1 - (UERJ) Para um mergulhador, cada 5 m de profundidade atingida corresponde a um acréscimo de 0,5 atm na pressão exercida sobre ele. Admita que esse mergulhador não consegue respirar quando sua caixa torácica está submetida a uma pressão acima de 1,02 atm.

Para respirar ar atmosférico por um tubo, a profundidade máxima, em cm, que pode ser atingida pela caixa torácica desse mergulhador é igual a:

a)   40.

b)   30.

c)   20.

d)   10.

e)   15.

Note e adote: ρ = 10³ kg/m³ e g = 10 m/s²

Resolução:

p₀  = 1 atm = 1×10⁵ N/m²

p = 1,02 atm = 1,02×10⁵ N/m²

ρ = 10³ kg/m³

g = 10 m/s²

p = p₀ + ρ⋅g⋅Δh

1,02×10⁵ = 1×10⁵   + 10³⋅10⋅Δh

1,02×10⁵ – 1×10⁵   = 10³⁺¹⋅Δh

0,02×10⁵ = 10⁴⋅Δh

Δh = 0,2 m = 0,2⋅100 cm = 20 cm

2 - (UERJ-RJ) Uma moeda é encontrada por um mergulhador no fundo plano de um lago, a 4 m de profundidade, com uma das faces, cuja área mede 12 cm², voltada para cima.

A força, em newtons, exercida sobre a face superior da moeda em repouso no fundo do lago equivale a:

a) 40

b) 48

c) 120

d) 168

e) 222

Resolução:

ρ = 10³ kg/m³

h = 4 m

g = 10 m/s²

1 m = 100 cm

10^{- 4} 

1 m² = (100 cm)² = 10 000 cm²

12 cm² = 12:10 000 m² = 0,0 012 m² = 12⋅10^{- 4} m²

p = ρ⋅g⋅h   ⇒   p = 10³⋅10⋅4 ⇒ p = 4⋅10⁴ N/m²

F = 4⋅10⁴⋅12⋅10^{- 4}    ⇒   F = 48⋅10^{4 + (- 4)}

F = 48⋅10^{4 - 4}   ⇒   F = 48⋅10⁰   ⇒   F = 48⋅1  

F = 48 N  

3 - (Unesp) A diferença de pressão máxima que o pulmão de um ser humano pode gerar por inspiração é em torno de 0,1⋅10⁵ 𝑃𝑎  ou 0,1 𝑎𝑡𝑚. Assim, mesmo com a ajuda de um snorkel (respiradouro), um mergulhador não pode ultrapassar uma profundidade máxima, já que a pressão sobre os pulmões aumenta à medida que ele mergulha mais fundo, impedindo-os de inflarem.

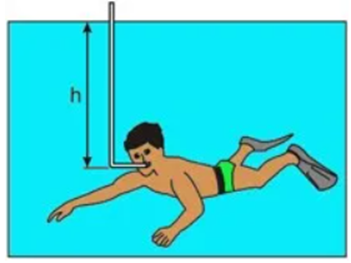
Considerando a densidade da água 10³ kg/m e a aceleração da gravidade 10 m/s², a profundidade máxima estimada, representada por h, que uma pessoa pode mergulhar respirando com a ajuda de um snorkel é igual a

A) 1,1 ‧ 10² m

B) 1,0 ‧ 10² m

C) 1,1 ‧ 10¹ m

D) 1,0 ‧ 10¹ m

E) 1,0 ‧ 10⁰ m

Resolução:

Δp = 0,1⋅10⁵ 𝑃𝑎

ρ = 10³ kg/m 

g = 10 m/s²

A diferença de pressão (Δp) pode ser dada pela lei de Stevin:

Δp = ρ⋅g⋅Δh ⇒ 0,1⋅10⁵ = 10³⋅10⋅Δh

0,1⋅10⁵ = 10³⋅10¹⋅Δh   ⇒ 0,1⋅10⁵ = 10⁴⋅Δh

Δh = 0,1⋅10^{5 –  4}   ⇒   Δh = 1,0⋅10^–1 ⋅10¹

Δh = 1,0⋅10^{–1 + 1}   ⇒   Δh = 1,0⋅10⁰ m

Resposta: Letra E

4 - (Uncisal) Em um laboratório, as substâncias são identificadas no rótulo pelo nome e por algumas propriedades químicas. No intuito de descobrir qual a substância armazenada num frasco no qual o rótulo foi retirado, um estudante aplicado de física propôs um experimento. Foram colocados num sistema constituído por vasos comunicantes o líquido desconhecido e álcool. Como são líquidos imiscíveis, é possível estimar a densidade do líquido medindo a altura das colunas líquidas a partir da superfície de separação desses líquidos. Esses valores são mostrados na figura a seguir. Consultando a tabela com os valores das densidades de alguns líquidos, disponível nesse laboratório, é provável que o líquido desconhecido seja:

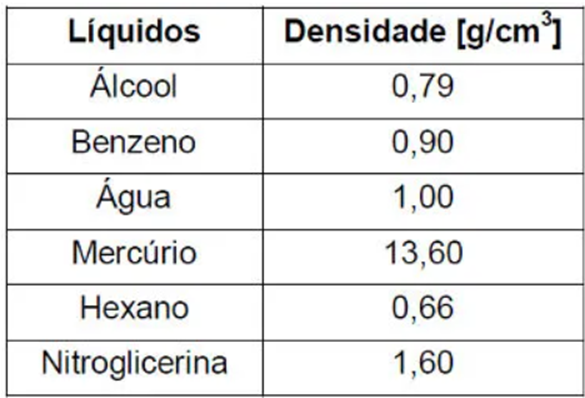
a) a nitroglicerina.

b) o hexano.

c) o mercúrio.

d) a água.

e) o benzeno.

Resolução:

Aplicando a lei de Stevin para o caso dos vasos comunicantes, o produto das alturas das colunas de líquido, determinadas de um mesmo ponto, pela densidade dos líquidos deve ser igual. Assim, podemos escrever que:

p_A= p_L

ρ_A = 0,79 g/cm³

h₁ = 0,270 m

h₂ = 0,237 m

𝜌_L= ?

Igualando as pressões do mesmo nível:

ρ_A⋅g⋅h₁ = 𝜌_L⋅𝑔⋅ℎ₂

ρA⋅g⋅h1 =ρ_L⋅𝑔⋅ℎ2

ρ_L= 0,9 g/cm³

Logo, o líquido desconhecido é o benzeno.

Resposta: Letra E

5 - (UEL) Um tubo em U, longo, aberto nas extremidades, contém mercúrio, de densidade 13,6 g/cm³. Em um dos ramos, coloca-se água, de densidade 1,0 g/cm³, até ocupar uma altura de 32 cm. No outro ramo coloca-se óleo, de densidade 0,8 g/cm³, que ocupa altura de 6,0 cm. O desnível entre as superfícies livres nos dois ramos, em cm, é de

a) 38.

b) 28.

c) 24.

d) 20.

e) 15.

Resolução:

ρ_A = 1,0 g/cm³

ρ_O = 0,8 g/ cm³

ρ_M = 13,6 g/ cm³

h_A = 32 cm

h_O = 6, 0 cm

No nível N:

p_A = p₀ + p_{M (A pressão da água é igual à pressão do óleo mais a pressão do mercúrio)}

ρ_A ⋅g⋅h_A= ρ_O⋅g⋅ρ_O + ρ_M ⋅g⋅h_M

Simplificando (Cancelando g nos dois membros):

ρ_A ⋅h_A= ρ_O⋅ρ_O + ρ_M ⋅h_M

1⋅32= 0,8⋅6 + 13,6⋅h_M

32 = 4,8 + 13,6⋅h_M

32 – 4,8 = 13,6⋅h_M

27,2 = 13,6⋅h_M

h_M = 2 cm

Como:

△x +6 + h_M = 32

△x + 6 + 2 = 32

△x = 32 – 2 – 6

△x = 24 cm

Resposta: Letra C

6 - (UFF-RJ) O sifão é um instrumento usado para a retirada de água de lugares de difícil acesso.

Como mostra a figura a seguir, seu funcionamento se baseia no fato de que, quando o tubo que liga os recipientes A e B está cheio, há uma diferença de pressão hidrostática entre os pontos P e Q, o que provoca um fluxo de água de A para B. Essa diferença de pressão depende da seguinte característica do nosso planeta:

a) pressão atmosférica.

b) aceleração da gravidade local.

c) temperatura da superfície.

d) densidade da atmosfera.

e) velocidade de rotação do planeta.

Resolução:

Vamos analisar essa questão por meio da fórmula do teorema de Stevin:

Δp = ρ⋅g⋅Δh

A diferença de pressão hidrostática entre P e Q em um sifão, que leva à transferência de água, depende da aceleração da gravidade local. 

Resposta: Letra B.