Desenho animado caseiro

Estou fazendo alguns experiências com desenhos  animados. Para a animação usei o PowerPoint e para transformar em vídeo, usei o Movie Maker.
O primeiro desenho intitulei de O caminhão. Fiz um desenho do caminhão no Paint utilizei uma apresentação do PowerPoint com 220 slides e depois usei o Movie Maker para transformar em vídeo:

O segundo desenho dei o título de Carros Vermelhos. Essa imagem do carro vermelho eu copiei do Google imagens e colei num slide do PowerPoint. A partir daí fui copiando e colando em outros slides, aumentando ou diminuindo o seu tamanho do desenho. No final usei a apresentação do PowerPoint com 342 slides:

 

Hidrostática - Lei de Stevin

A Lei de Stevin é um princípio fundamental da hidrostática que descreve a variação da pressão em um fluido em equilíbrio sob a influência da gravidade. Ela estabelece que a pressão em um ponto dentro de um líquido depende da profundidade e da densidade do fluido, sendo expressa pela equação:

p = p₀ + ρ⋅g⋅Δh   ou   Δp = ρ⋅g⋅Δh

Onde:

• ( p ) é a pressão em um ponto dentro do líquido,
• ( P₀ ) é a pressão na superfície do líquido (geralmente a pressão atmosférica),
• ( ρ ) é a densidade do fluido,
• ( g ) é a aceleração da gravidade,
• ( Δh ) é a profundidade do ponto abaixo da superfície do líquido,
• (Δp) é a variação da pressão.

Conceitos Importantes:

1. Pressão Hidrostática: A pressão aumenta à medida que a profundidade aumenta, devido ao peso da coluna de fluido acima do ponto analisado.
2. Independência da Forma do Recipiente: A pressão em um determinado nível depende apenas da profundidade e da densidade do fluido, não da forma do recipiente.
3. Aplicações: Esse princípio é essencial para engenharia hidráulica, cálculo de forças em barragens, mergulho submarino e até meteorologia, onde é usado para entender variações de pressão atmosférica.

Lembrando que:

m = µ ∙ V (sendo m = massa, µ = massa específica e V = volume)

A massa específica (µ) e a densidade (ρ) são grandezas físicas bem similares, já que ambas tratam a respeito da razão entre a massa e o volume. Contudo, enquanto a massa específica é a razão entre a massa da substância e o seu volume, a densidade é a razão entre a massa de um corpo e o seu volume.

A unidade de medida de pressão no sistema internacional é o N/m² (newton por metro quadrado), porém existem outros tipos de unidade de pressão, como atm (atmosfera), mmHg (milímetro de mercúrio), bar (bares), e pascal (Pa).

A relação entre as unidades de medida de pressão:

1 atm = 1,01325·10⁵ N/m² = 1,01325·10⁵ Pa = 760 mmHg = 1,01325 bar

Exemplos

1 - Qual a pressão em um ponto a 2 metros de profundidade em um lago, considerando a densidade da água como 1000 kg/m³ e a aceleração da gravidade como 10 m/s²? 

Resolução:

Aplicando a lei de Stevin:

Δp = ?

Δh = 2 m

g = 10 m/s²

𝜌 = 1000 kg/m³

Δp = 𝜌⋅𝑔⋅Δℎ

Δp = 1000⋅10⋅2

Δp = 20 000 Pa   ou   Δp = 20 kPa

2 - Um recipiente de 1,5 m está totalmente cheio de um líquido cuja densidade vale 1 200 kg/m³, e, no fundo dele, está uma moeda. Qual é o valor da pressão total sobre a moeda? Utilize a gravidade valendo 10 m/s².

Resolução

p₀ = 1,0⋅10⁵ N/m²

𝜌 = 1 200 kg/m³

g = 10 m/s²

Δh = 1,5 m

p = ?

p = p₀ + ρ⋅g⋅Δh

p = 1,0⋅10⁵ + 1 200⋅10⋅1,5

p = 1,0⋅10⁵ + 18 000

p = 1,0⋅10⁵ + 0,18⋅10⁵ 

p = 1,18⋅10⁵ N/m²

Exercícios

1 - (UERJ) Para um mergulhador, cada 5 m de profundidade atingida corresponde a um acréscimo de 0,5 atm na pressão exercida sobre ele. Admita que esse mergulhador não consegue respirar quando sua caixa torácica está submetida a uma pressão acima de 1,02 atm.

Para respirar ar atmosférico por um tubo, a profundidade máxima, em cm, que pode ser atingida pela caixa torácica desse mergulhador é igual a:

a)   40.

b)   30.

c)   20.

d)   10.

e)   15.

Note e adote: ρ = 10³ kg/m³ e g = 10 m/s²

Resolução:

p₀  = 1 atm = 1×10⁵ N/m²

p = 1,02 atm = 1,02×10⁵ N/m²

ρ = 10³ kg/m³

g = 10 m/s²

p = p₀ + ρ⋅g⋅Δh

1,02×10⁵ = 1×10⁵   + 10³⋅10⋅Δh

1,02×10⁵ – 1×10⁵   = 10³⁺¹⋅Δh

0,02×10⁵ = 10⁴⋅Δh

Δh = 0,2 m = 0,2⋅100 cm = 20 cm

2 - (UERJ-RJ) Uma moeda é encontrada por um mergulhador no fundo plano de um lago, a 4 m de profundidade, com uma das faces, cuja área mede 12 cm², voltada para cima.

A força, em newtons, exercida sobre a face superior da moeda em repouso no fundo do lago equivale a:

a) 40

b) 48

c) 120

d) 168

e) 222

Resolução:

ρ = 10³ kg/m³

h = 4 m

g = 10 m/s²

1 m = 100 cm

10^{- 4} 

1 m² = (100 cm)² = 10 000 cm²

12 cm² = 12:10 000 m² = 0,0 012 m² = 12⋅10^{- 4} m²

p = ρ⋅g⋅h   ⇒   p = 10³⋅10⋅4 ⇒ p = 4⋅10⁴ N/m²

F = 4⋅10⁴⋅12⋅10^{- 4}    ⇒   F = 48⋅10^{4 + (- 4)}

F = 48⋅10^{4 - 4}   ⇒   F = 48⋅10⁰   ⇒   F = 48⋅1  

F = 48 N  

3 - (Unesp) A diferença de pressão máxima que o pulmão de um ser humano pode gerar por inspiração é em torno de 0,1⋅10⁵ 𝑃𝑎  ou 0,1 𝑎𝑡𝑚. Assim, mesmo com a ajuda de um snorkel (respiradouro), um mergulhador não pode ultrapassar uma profundidade máxima, já que a pressão sobre os pulmões aumenta à medida que ele mergulha mais fundo, impedindo-os de inflarem.

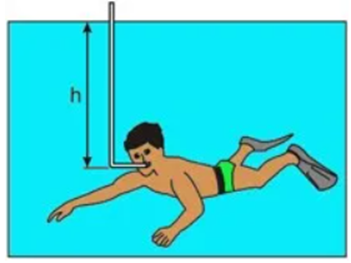
Considerando a densidade da água 10³ kg/m e a aceleração da gravidade 10 m/s², a profundidade máxima estimada, representada por h, que uma pessoa pode mergulhar respirando com a ajuda de um snorkel é igual a

A) 1,1 ‧ 10² m

B) 1,0 ‧ 10² m

C) 1,1 ‧ 10¹ m

D) 1,0 ‧ 10¹ m

E) 1,0 ‧ 10⁰ m

Resolução:

Δp = 0,1⋅10⁵ 𝑃𝑎

ρ = 10³ kg/m 

g = 10 m/s²

A diferença de pressão (Δp) pode ser dada pela lei de Stevin:

Δp = ρ⋅g⋅Δh ⇒ 0,1⋅10⁵ = 10³⋅10⋅Δh

0,1⋅10⁵ = 10³⋅10¹⋅Δh   ⇒ 0,1⋅10⁵ = 10⁴⋅Δh

Δh = 0,1⋅10^{5 –  4}   ⇒   Δh = 1,0⋅10^–1 ⋅10¹

Δh = 1,0⋅10^{–1 + 1}   ⇒   Δh = 1,0⋅10⁰ m

Resposta: Letra E

4 - (Uncisal) Em um laboratório, as substâncias são identificadas no rótulo pelo nome e por algumas propriedades químicas. No intuito de descobrir qual a substância armazenada num frasco no qual o rótulo foi retirado, um estudante aplicado de física propôs um experimento. Foram colocados num sistema constituído por vasos comunicantes o líquido desconhecido e álcool. Como são líquidos imiscíveis, é possível estimar a densidade do líquido medindo a altura das colunas líquidas a partir da superfície de separação desses líquidos. Esses valores são mostrados na figura a seguir. Consultando a tabela com os valores das densidades de alguns líquidos, disponível nesse laboratório, é provável que o líquido desconhecido seja:

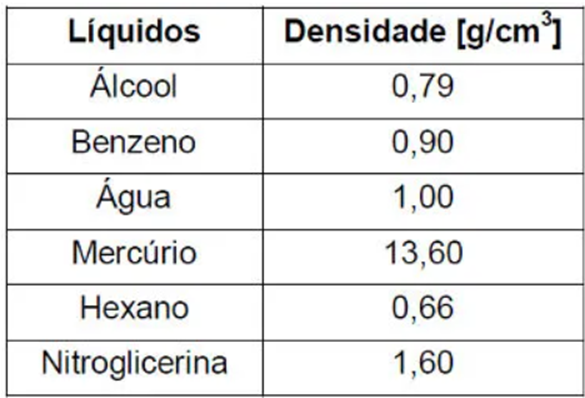
a) a nitroglicerina.

b) o hexano.

c) o mercúrio.

d) a água.

e) o benzeno.

Resolução:

Aplicando a lei de Stevin para o caso dos vasos comunicantes, o produto das alturas das colunas de líquido, determinadas de um mesmo ponto, pela densidade dos líquidos deve ser igual. Assim, podemos escrever que:

p_A= p_L

ρ_A = 0,79 g/cm³

h₁ = 0,270 m

h₂ = 0,237 m

𝜌_L= ?

Igualando as pressões do mesmo nível:

ρ_A⋅g⋅h₁ = 𝜌_L⋅𝑔⋅ℎ₂

ρA⋅g⋅h1 =ρ_L⋅𝑔⋅ℎ2

ρ_L= 0,9 g/cm³

Logo, o líquido desconhecido é o benzeno.

Resposta: Letra E

5 - (UEL) Um tubo em U, longo, aberto nas extremidades, contém mercúrio, de densidade 13,6 g/cm³. Em um dos ramos, coloca-se água, de densidade 1,0 g/cm³, até ocupar uma altura de 32 cm. No outro ramo coloca-se óleo, de densidade 0,8 g/cm³, que ocupa altura de 6,0 cm. O desnível entre as superfícies livres nos dois ramos, em cm, é de

a) 38.

b) 28.

c) 24.

d) 20.

e) 15.

Resolução:

ρ_A = 1,0 g/cm³

ρ_O = 0,8 g/ cm³

ρ_M = 13,6 g/ cm³

h_A = 32 cm

h_O = 6, 0 cm

No nível N:

p_A = p₀ + p_{M (A pressão da água é igual à pressão do óleo mais a pressão do mercúrio)}

ρ_A ⋅g⋅h_A= ρ_O⋅g⋅ρ_O + ρ_M ⋅g⋅h_M

Simplificando (Cancelando g nos dois membros):

ρ_A ⋅h_A= ρ_O⋅ρ_O + ρ_M ⋅h_M

1⋅32= 0,8⋅6 + 13,6⋅h_M

32 = 4,8 + 13,6⋅h_M

32 – 4,8 = 13,6⋅h_M

27,2 = 13,6⋅h_M

h_M = 2 cm

Como:

△x +6 + h_M = 32

△x + 6 + 2 = 32

△x = 32 – 2 – 6

△x = 24 cm

Resposta: Letra C

6 - (UFF-RJ) O sifão é um instrumento usado para a retirada de água de lugares de difícil acesso.

Como mostra a figura a seguir, seu funcionamento se baseia no fato de que, quando o tubo que liga os recipientes A e B está cheio, há uma diferença de pressão hidrostática entre os pontos P e Q, o que provoca um fluxo de água de A para B. Essa diferença de pressão depende da seguinte característica do nosso planeta:

a) pressão atmosférica.

b) aceleração da gravidade local.

c) temperatura da superfície.

d) densidade da atmosfera.

e) velocidade de rotação do planeta.

Resolução:

Vamos analisar essa questão por meio da fórmula do teorema de Stevin:

Δp = ρ⋅g⋅Δh

A diferença de pressão hidrostática entre P e Q em um sifão, que leva à transferência de água, depende da aceleração da gravidade local. 

Resposta: Letra B.

O Princípio de Arquimedes

Posted: 12 Feb 2016 06:38 AM PST Quando estamos na piscina temos a sensação de que somos menos pesados, não é mesmo? Na verdade nosso peso real não muda, existe uma força chamada empuxo que é responsável por esse “fenômeno” e sem a qual isso não ocorreria. Vamos compreender no artigo de hoje o princípio de Arquimedes, conteúdo da Física, para entender essa sensação tão divertida! Empuxo Todo corpo imerso em um líquido em equilíbrio, sofre uma força (denominada empuxo) que age na vertical, para cima, e tem intensidade igual ao peso do líquido deslocado. Na prática, conseguimos saber o volume de objetos de formas irregulares mergulhando esse objeto em um líquido contido em um recipiente de volume graduado, a variação na marcação do volume será o volume desconhecido do objeto. Supondo que um recipiente cilíndrico está totalmente cheio de água, ao colocarmos um cubo maciço dentro do recipiente parte da água irá derramar, se captarmos a água que derramou e pesarmos em uma balança obtemos o peso do líquido deslocado que como mencionado anteriormente possui o mesmo valor da força de empuxo(E). Demonstração: Lembrando que a direção e sentido da força de empuxo são sempre na vertical e para cima! Para casos onde o corpo não está totalmente submerso o volume do líquido deslocado não é igual ao volume do corpo, mas é igual a uma parte dele. Exemplo: Um cubo de densidade 0,8 g/cm³ está parcialmente submerso em um recipiente com água de densidade 1g/cm³ , visto de frente, 8 cm de aresta estão fora do líquido, qual o tamanho total da aresta do cubo? d: densidade do cubo V: Volume do cubo µ: densidade do líquido VLD: Volume da parte submersa h: tamanho total da aresta Flutua ou afunda? O objeto irá afundar se a força peso for maior que a força de empuxo; O objeto irá flutuar se a força peso for menor que a força de empuxo; O objeto ficará em equilíbrio se a força peso tiver o mesmo valor que a força de empuxo; Peso Aparente Peso aparente é aquele que sentimos quando estamos na piscina, como falamos no começo, ele é menor que o peso real, pois subtraímos o empuxo sofrido pelo corpo. O corpo quando no interior de um fluido exibe um peso aparente dado por: Peso aparente = Peso real – Empuxo O post Entenda o Princípio de Arquimedes apareceu primeiro no infoEnem.

Diferença entre Calor Específico e de Capacidade Térmica

Posted: 17 Feb 2016 09:42 AM PST Neste artigo abordaremos novamente a termologia. Assim como estudamos a diferença entre calor e temperatura (confira aqui), veremos a diferença entre capacidade térmica e calor específico. Do mesmo modo do artigo anterior, a compreensão destes conceitos torna-se fundamental para a resolução de problemas mais complexos dentro dessa área tão cobrado no Enem. Calor Específico O calor específico de uma substância (c) é uma grandeza física intensiva, ou seja, se trata de uma grandeza que não varia com as dimensões da substância. Assim, 1 e 100 litros de água possuem o mesmo calor específico. Por definição, o calor específico é a quantidade de calor necessária para que seja possível elevar a temperatura de uma determinada substância por unidade de temperatura. A unidade do sistema internacional é o joule por quilograma por kelvin – J/(kg.K) – mas a unidade mais comum é a caloria por grama por grau Celsius – cal/g.ºC – sendo que atualmente a grande maioria destes valores já se encontram tabelados. Esta definição pode ser usada para explicar, por exemplo, o motivo do cobre ser aquecido de maneira mais fácil que a água, uma vez que o calor especifico da água é maior que o do cobre, demandando uma maior energia para que obtenha a mesma temperatura. Capacidade Térmica Já a capacidade térmica ou capacidade calorífica de uma substância (C) é uma grandeza física extensiva, sendo que é dependente da massa de sua respectiva substância. Deste modo, já vimos que 1 e 100 litros de água possuem o mesmo calor específico, porém apresentam capacidades térmicas diferentes, sendo que os 100 litros terão uma maior capacidade calorífica. Sua definição nos traz que a capacidade térmica é a quantidade de calor necessária (cedida ou recebida) para que um corpo varie sua temperatura em uma unidade. A capacidade calorífica de um corpo é expressa em Joule por Kelvin (J/K), mas frequentemente encontrada como caloria por grau Celsius (cal/ºC). Podemos ainda estabelecer uma relação entre a capacidade térmica e o calor específico de um corpo, desde que este apresente uma única substância. Através da equação fundamental da calorimetria e da definição de capacidade térmica temos que: Onde m é a massa do corpo, c é seu calor específico e C é a capacidade calorífica. Podemos então notar que a capacidade térmica será dependente das propriedades do material e também de seu volume, enquanto o calor específico depende apenas das propriedades da substância. O post Saiba Diferenciar Calor Específico de Capacidade Térmica apareceu primeiro no infoEnem.