Arranjo condicional

Um arranjo condicional, em análise combinatória, é um tipo de arranjo onde, além da ordem dos elementos importar, há uma condição adicional que precisa ser satisfeita. Diferentemente dos arranjos simples, que não possuem restrições, os arranjos condicionais impõem uma condição que deve ser seguida na formação dos agrupamentos. 

Exemplos:

1 - Imagine que temos 5 cores diferentes para pintar uma bandeira, e queremos saber de quantas maneiras podemos pintá-la, sabendo que a primeira faixa deve ser sempre vermelha. Neste caso, a condição é que a primeira faixa seja vermelha.

Solução:

• Identificar a condição: A primeira faixa deve ser vermelha.
• Considerar as possibilidades restantes: Depois de pintar a primeira faixa de vermelho, restam 4 cores para as outras faixas.

• Aplicar o princípio multiplicativo: Para cada cor da primeira faixa (1 possibilidade), temos 4 possibilidades para a segunda faixa, 3 para a terceira, e assim por diante. Portanto, o número total de maneiras é 1 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24.

2 - Imagine que você quer formar grupos de 4 alunos a partir de um grupo de 10, com a condição de que dois alunos específicos (A e B) não podem estar no mesmo grupo. 

Solução:

Este é um exemplo de arranjo condicional. A ordem dos alunos no grupo importa, então é um arranjo, e a condição de que A e B não podem estar no mesmo grupo limita as possibilidades, tornando-o um arranjo condicional.

Para resolver este tipo de problema, uma estratégia útil é calcular o total de arranjos sem a condição e depois subtrair os arranjos que não cumprem a condição.

• Total de arranjos sem a condição:

A quantidade total de arranjos de 4 alunos escolhidos de um grupo de 10 é um arranjo de 10 elementos tomados de 4 em 4, que se calcula como:

• Arranjos onde A e B estão no mesmo grupo:

Se A e B estão juntos, podemos considerar eles como um único elemento. Então, estamos formando um grupo de 3 elementos, sendo um deles a dupla (A,B) e os outros dois escolhidos dos 8 alunos restantes.
A ordem dos elementos importa, então temos um arranjo de 3 elementos. A dupla (A,B) pode ocupar a primeira, segunda ou terceira posição no grupo.

(escolhendo os dois outros alunos)

• Como (A,B) pode estar em qualquer ordem, temos 2! = 2 possibilidades para a dupla.

Total de arranjos onde A e B estão juntos: 56 ⋅ 2 = 112

• Arranjos que cumprem a condição (A e B não estão juntos):

Subtraímos os arranjos onde A e B estão juntos do total de arranjos:

5040 – 112 = 4 928

Portanto, existem 4 928 maneiras de formar grupos de 4 alunos, onde A e B não estão no mesmo grupo, considerando que a ordem dos alunos no grupo importa.

Exercícios

1 - Quantos arranjos com 4 elementos do conjunto {A,B,C,D,E,F} começam com duas letras do subconjunto {D,E,F}?

Resolução:

• Vamos escolher as duas primeiras letras:

Temos 3 opções para a primeira letra (D, E ou F) e 2 opções para a segunda letra (as duas restantes de D, E, F).

• Vamos escolher as duas letras restantes:

Para as duas letras restantes, podemos escolher qualquer uma das 4 letras restantes (A, B, C e a que não foi escolhida de D, E, F).

• Total de arranjos:

Multiplicamos o número de maneiras de escolher as primeiras duas letras pelo número de maneiras de escolher as últimas duas letras:

2 – Com os algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, tomados 6 a 6, quantos números podem ser formados tendo nas duas posições iniciais algarismos distintos que são números ímpares?

Resolução:

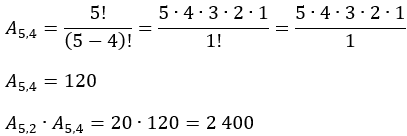
3 – Com os algarismos: 1, 2, 3, 4, 5, 6, tomados 4 a 4, quantos números podem ser formados tendo nas duas posições iniciais algarismos pares repetidos ou não?

Resolução:

4 - Quantas maneiras há de arranjar 5 pessoas em uma fila, se 2 pessoas específicas devem ficar juntas?

Resolução:

Sem restrições, o número total de maneiras de organizar 5 pessoas em uma fila é dado pelo fatorial:

5! = 5⋅4⋅3⋅2⋅1 = 120

Agora, considerando que duas pessoas específicas devem ficar juntas, podemos tratá-las como um único "bloco". Assim, em vez de organizar 5 indivíduos separadamente, agora temos 4 elementos para organizar: o "bloco" das duas pessoas e os outros três indivíduos.

O número de maneiras de organizar esses 4 elementos é:
4! = 4⋅3⋅2⋅1 = 24

Dentro do "bloco", as duas pessoas podem trocar de lugar entre si, o que adiciona mais possibilidades:
2! = 2⋅1 = 2

Portanto, o número total de maneiras de organizar essa fila, garantindo que as duas pessoas estejam juntas, é:
24⋅2 = 48

Então, há 48 maneiras de arranjar essas 5 pessoas mantendo as duas específicas sempre juntas.