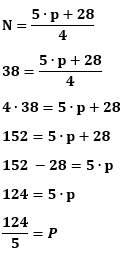Exercícios com porcentagem

 

Pontos no plano cartesiano

Exercícios resolvidos

1 – Complete os pares ordenados, com as coordenadas cartesianas dos pontos marcados, no desenho:

                       A(     ,     ), B(     ,     ), C(     ,     ), D(     ,     ) e E(     ,     )

Resposta:

A( 2 , 3 ), B( – 3 , 4 ), C(  3 , 2 ), D( – 4 , – 1 ) e E( 2 , – 3 )

2 – Localize no plano  cartesiano abaixo os pontos de coordenadas A( 2 , 3 ), 
B( – 2 , 3 ), C( 1 , – 2 ),  D( – 4 , – 2 ) e E( 3 , 0 ).

Resolução:

3 – No plano cartesiano da figura, localize os pontos A (2,3), B(–1, –2), C(–2,4), D(3,1), E(2, –3), 

F(2, – 2) e G(–1,0).

Resolução:

Exercícios com ângulos suplementares

1 – Dois ângulos são suplementares. Se um deles tem medida de 20º, qual a medida do outro? 

x + 20º = 180º

x = 180º – 20º

x = 160º

2 – Vamos calcular o valor de x nas figuras abaixo:

a) 

3x + 10º + 50º = 180º

3x + 60º = 180º

3x = 180º –  60º

3x = 120º

x = 120º/3

x = 40º

b) 

x + 90º + 2x = 180º

x + 2x = 180º – 90º

x + 2x = 180º – 90º

3x = 90º

x = 90º/3

x = 30º

       


c) 

2x + 20º + 2x = 180º

2x + 2x = 180º – 20º

4x = 160º

x = 160º/4

x = 40º

Exercícios com soma dos ângulos internos de um triângulo

2 – Calcule a medida do ângulo C no triângulo abaixo.

A + B + C = 180^o

68^o + 90^o + C = 180^o

C = 180^o  – 68^o – 90^o 

C = 22^o

3 – O desenho da figura abaixo é um triângulo isósceles.

     


      a)    Qual é o seu perímetro?

Perímetro é a soma dos lados:

P = 10 cm + 10 cm + 6 cm

P = 26 cm

      b)   Calcule a medida do 

            ângulo A.

A + B + C = 180^o

A + 65^o + 65^o = 180^o

A + 130^o = 180^o

A = 180^o – 130^o

A = 50^o

Exercícios com ângulos complementares

Ângulos complementares são dois ângulos cuja soma é igual a 90 graus. Em outras palavras, se você somar as medidas de dois ângulos complementares, o resultado será sempre 90°.

Exercícios

1 – Calcular o valor de x na figura abaixo, sabendo que os dois ângulos somam 90º.

Resolução:

2 – Calcular o valor de x na figura abaixo, sabendo que os três ângulos somam 90º.

Resolução:

X = 12°

Resposta: Letra B

3 – Calcular os valores dos quatro ângulos na figura.

Resolução:

Cálculos dos ângulos:

Resposta: Os ângulos medem 10°, 15°, 30° e 35°.

4 – Os ângulos das figuras abaixo são complementares. Calcule o valor de cada ângulo indicado:

Resolução:

a)

Resposta: 65° e 25°

Resposta: 60° e 30°

Figuras de fractais

Atividades desenvolvidas por alunos, na Mostra Cultural da Escola Madre Francisca - outubro/2018.

Fórmula de Tanner

 O pediatra britânico James Mourilyan Tanner, mundialmente conhecido pelas suas pesquisas sobre o crescimento normal e patológico e pela escala de avaliação do desenvolvimento puberal. Criou nos anos 1960 uma fórmula para estimar até que altura uma criança vai crescer, tomando como parâmetros a altura dos pais. Essa fórmula, que recebeu o nome de seu criador, Fórmula de Tanner, varia para o cálculo da altura de meninos em relação ao cálculo da altura de meninas. A fórmula Tanner  faz uma projeção, mas a principal influência para determinar a altura das crianças é  a hereditariedade. Existe, nesse cálculo, uma margem de erro de mais ou menos de 10% para cima ou para baixo.

👨 Para meninos:

👩 Para meninas:

 

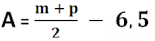
Considere em centímetros:

A: altura da criança

M: altura da mãe

P: altura do pai

Exemplo: De acordo com a fórmula, sabendo que um pai tem 1,72 m (172 cm) e uma  mãe tem 1,50 m (150 cm):

a)   Até que altura estima-se que um menino, filho do casal, vai crescer?

Para menino, vamos usar a fórmula:

A = 167,5 cm

ou aproximadamente

A = 1,68 m

b) Até que altura estima-se que uma menina, filha do casal, vai crescer?

Para menina, vamos usar a fórmula:

A = 154,5 cm

ou aproximadamente

A = 1,55 m

Unidade de medida de calçado

Com a unidade de medida de calçado padronizada é possível que uma relação entre o número do calçado (N) e o comprimento do pé (p), em centímetros.

No Brasil, por exemplo, podemos estabelecer essa relação por meio de uma fórmula:

Exemplos:
1 - Utilizando essa fórmula, vamos determinar o número do calçado para uma criança cujo comprimento do pé é de 22 cm. 

Fazendo p = 22 cm, vamos ter:

Ou seja, o número do calçado dessa criança deverá ser 28.

 2- Qual é o comprimento do pé de uma pessoa que usa uma calçado de número 38?

 Fazendo N = 38, vamos ter:

p = 24,8 cm

Probabilidade de eventos na genética

Posted: 25 Feb 2019 02:22 AM PST

O assunto a seguir costuma ser cobrado nos mais diversos vestibulares, assim como no Enem. Estudar a probabilidade de eventos na genética requer a mistura de conhecimentos em duas disciplinas (Matemática e Biologia), e é isso que faremos a seguir! Serão apresentadas algumas definições importantes, além da explicação sobre o cálculo.

Falando de genética, devemos entender primeiramente o que é um gene. Os genes são pequenas partículas que carregam o material genético (DNA) e que produzem proteínas que transmitirão o material genético dos pais para os filhos.

O nosso interesse será nos genes alelos, que são pares de genes, os quais se unem de maneira a formar uma determinada característica do filho. Nesse par, um gene é proveniente da mãe (do óvulo), e o outro é transmitido pelo pai (através do espermatozoide).

Genes Alelos Recessivos

Os genes alelos podem ser classificados de diferentes maneiras, as quais vamos citar a classificação quanto a dominância. Os genes alelos recessivos são aqueles em que a característica física (fenótipo) se manifesta somente em situações onde não existem genes dominantes. Os genes recessivos são representados por letras minúsculas (aa, bb e vv) e como falamos, a característica física só será expressa em situações de homozigose, que são justamente os pares que mostramos acima!

Os genes recessivos estão ligados a características como olhos azuis, cabelos ruivos e loiros, nariz reto, incapacidade de enrolar a língua, entre outros. E também a algumas doenças, tais como a miopia, o daltonismo, o albinismo e a hemofilia.

Genes Alelos Dominantes

Já os genes alelos dominantes são representados por aqueles em que a característica do fenótipo ocorre em sua presença, seja em casos onde os pares são iguais (homozigose), ou casos em que existem um gene dominante e um recessivo, o que recebe o nome de heterozigose! Os genes dominantes são representados pelas letras maiúsculas (AA, BB e VV), porém, a sua característica fenotípica será representada pelos pares AA, Aa, BB, Bb, VV e Vv.

Entre as características associadas aos genes dominantes estão: Lábios grossos, cabelo e olhos escuros, calvície, polegar e dedo mindinho curvados, entre outros. E também doenças associadas, como polidactilia e doença de von Hippel.

Como foi mostrado, as características estão associadas aos genes dominantes e recessivos e, portanto, de cada cruzamento de genes teremos probabilidades diferentes para a ocorrência do evento. Para isso, vamos considerar a possibilidade de um filho possuir olhos azuis, cujo gene formador é homozigoto recessivo (aa), e os pais possuem olhos castanhos, com genes heterozigotos dominantes (Aa). Desta forma, vamos agrupar as combinações possíveis na tabela a seguir:

Dessa forma, temos um caso homozigoto recessivo, que resultaria em um filho de olhos azuis, enquanto temos um evento homozigoto dominante e dois heterozigotos, também dominantes. Assim, temos quatro eventos possíveis, sendo que em um deles temos o caso desejado. A probabilidade desta ocorrência é então:

Enquanto que a probabilidade de os olhos serem castanhos representa os 75% restantes. Portanto, a probabilidade de ocorrência de determinadas características físicas está diretamente ligada com a dominância dos genes dos pais.

Com isso, é possível utilizar os seus conhecimentos em matemática para realizar as combinações possíveis, além de determinar a chance de sua ocorrência.

O post ESTUDANDO A PROBABILIDADE NA GENÉTICA apareceu primeiro no infoEnem. 

Blindagem eletrostática e a Gaiola de Faraday

Posted: 26 Feb 2019 02:52 AM PST

Na postagem de hoje vamos estudar sobre um importante conceito dentro da área da eletricidade, que é a blindagem eletrostática. Vamos explicar como se dá o seu funcionamento, além de apresentar o seu exemplo mais famoso, a gaiola de Faraday.

Um corpo condutor pode ser eletrizado de três maneiras diferentes, seja por contato, indução ou atrito (você pode relembrar aqui). Ao ser eletrizado, as cargas elétricas presentes no corpo irão se dividir uniformemente através da superfície do corpo, uma vez que as cargas tendem a se afastar devido a repulsa das cargas de mesmo sinal. Ao atingir um nível de equilíbrio, onde não haverá a movimentação destas cargas, dizemos que a superfície atingiu o equilíbrio eletrostático.

Entre as propriedades de uma superfície condutora que esteja em equilíbrio eletrostático, a que vamos destacar é a blindagem eletrostática. A blindagem eletrostática afirma que o campo elétrico no interior da superfície condutora seja nulo, o que ocorre devido a distribuição equitativa das cargas, as quais falamos anteriormente.

E qual as vantagens desse fenômeno? São várias! A blindagem eletrostática é utilizada para proteger equipamentos que não podem sofrer a ação de cargas elétricas internas, como as televisões e rádios, que possuem suas superfícies eletrônicas envolvidas por uma superfície metálica, de modo a evitar a interferência de campos elétricos e magnéticos externos, o que poderia levar ao mal funcionamento de seus componentes.

Outra aplicação importantíssima está nos automóveis e aviões. Devido a blindagem eletrostática dos veículos, que possuem de maneira simplificada uma esfera de metal condutor (lataria do veículo) sobre um material isolante (pneus), é possível estar em segurança na ocorrência de acidentes com a rede elétrica por exemplo. Nessas situações, é necessário que os ocupantes permaneçam dentro do veículo até o desligamento da eletricidade, pois ao saírem a blindagem será rompida e o ocupante receberá uma forte descarga elétrica. Este mesmo conceito, aplicado aos aviões, permite as viagens na ocorrência de raios, pois a superfície metálica do avião funcionará de maneira que seu interior não possua nenhuma carga elétrica!

Gaiola de Faraday

A descoberta e comprovação da blindagem eletrostática foi feita pelo físico e químico inglês Michael Faraday(1791-1867). Faraday, no ano de 1836, entrou em uma gaiola de material condutor e se sentou em uma cadeira, feita de um material isolante, como madeira e borracha. Na sequência, a gaiola foi devidamente fechada e submetida a descargas elétricas. Como esperado, nada aconteceu com o físico. Esse experimento, ficou mundialmente conhecido como Gaiola de Faraday. A seguir temos uma imagem de uma gaiola de Faraday, similar ao utilizado no primeiro experimento.

Atualmente existem diversos eventos e locais que permitem você observar (e até mesmo testar, se tiver vontade!) uma Gaiola de Faraday. Embora esteja completamente provado que o corpo no interior de um condutor permaneça isolado devido a distribuição de cargas em sua superfície, não são todas as pessoas que possuem coragem para comprovar isso!

Os conceitos de blindagem eletrostática e a Gaiola de Faraday não apresentam equações, porém o seu entendimento está muito presente em situações de nosso dia a dia, além de envolver diversos conceitos da eletricidade, sendo uma figura quase certa em vestibulares. Portanto, é importante entendermos mais esse conceito muito interessante, além de suas aplicações!

O post BLINDAGEM ELETROSTÁTICA E A GAIOLA DE FARADAY apareceu primeiro no infoEnem.