Exercícios com teorema de Pitágoras

O teorema de Pitágoras é considerado uma das principais descobertas da Matemática, ele descreve uma relação existente no triângulo retângulo. O triângulo retângulo pode ser identificado pela existência de um ângulo reto, isto é, medida de 90º. Os lados do triângulo retângulo recebem nomes especiais: o maior lado é chamado de hipotenusa que é oposto ao ângulo reto e os lados menores chamados de catetos:

          

Teorema: O quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

          

      Exercícios

1 - Determine a medida desconhecida da hipotenusa no triângulo retângulo da figura abaixo:                            

Resolução:
• Pelo teorema de Pitágoras temos:
a² = b² + c²
x² = 4² + 3²
x² = 4·4 + 3·3
x² = 16 + 9
x² = 25

x = 5

2 - Calcule a medida x no triângulo da figura.

          

Resolução:

• Pelo teorema de Pitágoras temos:

a² = b² + c²

a² = b² + c²

 x² = 9² + 12²

 x² = 9·9 + 12·12

x² = 81 + 144

x² = 225

3 - Calcule a medida desconhecida do cateto no triângulo retângulo da figura abaixo.

          

Resolução:
• Pelo teorema de Pitágoras temos:

4 – Os catetos de um triângulo retângulo medem 5 cm e 12 cm. Determine sua hipotenusa.

Resolução:

• Usando o teorema de Pitágoras:

• Resposta: A medida da hipotenusa desse triângulo é de 13 cm.

5 – Qual é o valor de x?

          

Resolução:

• Usando o teorema de Pitágoras:

a²  = b² + c²
(3x – 2)²  = (2x – 2)² + x²
(3x)²  – 2⋅3x⋅2 + 2² = (2x)²  + 2⋅2x⋅2 + 2² + x²

9x² –12x + 4 = 4x² + 8x + 4 + x²
9x² – 4x² – x² – 12x – 8x = 4 – 4
4x²  – 20x = 0     : (4x)
x – 5 = 0  
x = 5

6 - Calcule as medidas desconhecidas dos lados do triângulo da figura.

          

Resolução:

• Pelo teorema de Pitágoras temos:
a²  = b² + c²
(x + 4)² = x² + (x + 2)²
x² + 2⋅x⋅4 + 4² = x² + x² + 2⋅x⋅2 + 2²

x² + 8x + 16 = x² + x² + 4x + 4
x² – x² – x² + 8x – 4x + 16 – 4
– x² + 4x + 12 = 0    ✕(– 1)
x² – 4x – 12 = 0

• Usando a fórmula de Bhaskara:

a = 1,    b = – 4   e   c = – 12 

• Como os lados do triângulo tem medidas x, x + 2 e x + 4:

x = 6

x + 2 ⇾  6 + 2 = 8
x + 4 ⇾  6 + 4 = 10

• Resposta: Os lados do triângulo são 6, 8 e 10.

7 - Em uma rua horizontal, a companhia elétrica de uma cidade vai estender um cabo partindo de um poste vertical ao solo, cuja altura é 7 metros, até uma casa, conforme a ilustração.

          

Se o topo da casa está a 3 m do solo e a distância do poste à casa é 12 m, qual é o comprimento aproximado do cabo? Adote √10 = 3,2 e uma casa decimal para aproximação.​

Resolução:

          

• Usando o teorema de Pitágoras:

• Resposta: O comprimento aproximado do cabo é de 12,8 metros.  

8 - (Fuvest) Na figura a seguir, ABC é um triângulo isósceles e retângulo em A, e PQRS é um quadrado de lado

          

Então, a medida do lado AB é:

a) 1           b) 2           c) 3           d) 4           e) 5

Resolução:

• Os triângulos BPS e QCR também são retângulos isósceles. Logo, os segmentos BP e QC são iguais a SP e RQ, respectivamente. Consequentemente, os segmentos BP, PQ e QC possuem a mesma medida. Portanto, a medida do lado BC é igual a 3 vezes a medida do lado do quadrado, ou seja:

          

• Considerando os lados AB e AC iguais a x, e utilizando o teorema de Pitágoras:

          

  

9 - (Unesp) Uma gangorra é formada por uma haste rígida AB, apoiada sobre uma mureta de concreto no ponto C, como na figura. Quando a extremidade B da haste toca o chão, a altura da extremidade A em relação ao chão é:

Resolução:

Cálculo da altura H₁:

Usando o teorema de Pitágoras no triângulo CEG:

Os triângulos CEG e ABF são semelhantes:

Multiplicando cruzado:

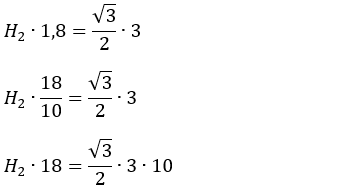
Simplificando as frações:

Resposta: Letra D