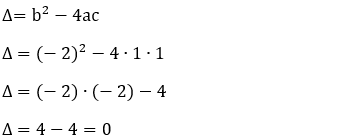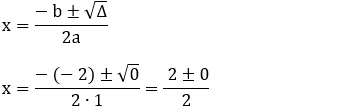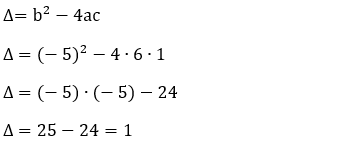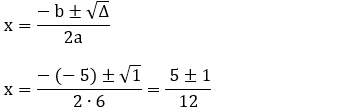A energia mecânica é a soma da energia cinética e da energia potencial de um sistema. Ela representa a capacidade de um objeto realizar trabalho devido ao seu movimento ou posição. Em um sistema conservativo, onde não há forças dissipativas como atrito ou resistência do ar, a energia mecânica total permanece constante.
A equação que descreve a energia mecânica é:
Em = EC + Ep
Onde:
- ( Em)
é a energia mecânica total
- ( EC
) é a energia cinética
- ( Ep
) é a energia potencial (pode ser gravitacional ou elástica, dependendo do
contexto)
Conceitos Importantes:
· Conservação da Energia Mecânica: Em sistemas sem forças dissipativas, a energia mecânica se conserva, ou seja, a energia cinética pode se transformar em energia potencial e vice-versa, mas sua soma continua a mesma.
· Transformação de Energia: Em situações reais, forças como o atrito podem transformar a energia mecânica em calor, reduzindo a energia disponível para movimento.
· Aplicações: A energia mecânica é essencial na análise do movimento de objetos, máquinas, esportes, engenharia civil e até fenômenos naturais como a trajetória dos planetas.
Exemplos
1 - (PUC-RJ) Determine a massa de um avião viajando a
720 km/h, a uma altura de 3000 m do solo, cuja
energia mecânica total é de 70,0⋅106 J. Considere a
energia potencial gravitacional como zero no solo. (g =10 m/s2)
a) 1 000 kg
b) 1 400 kg
c) 2 800 kg
d) 5 000 kg
e) 10 000 kg
v = 720 km/h = 720:3,6 m/s = 200 m/s
h = 3 000 m
Em = 70,0⋅106 J
Ep = m⋅g⋅h
Em
= EC + Ep
Colocando "m" em evidência:
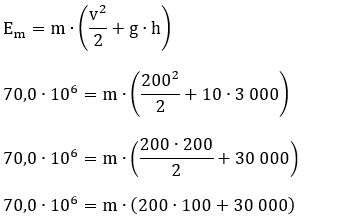

m = 14,0⋅102 ⇒ m = 14,0⋅10⋅10
m = 14,0⋅100 ⇒ m = 1 400 kg
2 - (Udesc) Deixa-se
cair um objeto de massa 500 g de uma altura de 5 m acima do solo. Assinale a
alternativa que representa a velocidade do objeto, imediatamente, antes de
tocar o solo, desprezando-se a resistência do ar.
a) 10 m/s
b) 7,0 m/s
c) 5,0 m/s
d) 15 m/s
e) 2,5 m/s
Resolução:
m = 500 g
h = 5 m
g = 10 m/s2
v = ?
Energia mecânica na altura máxima:
v0 = 0
Em = EC + Ep
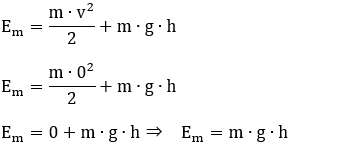

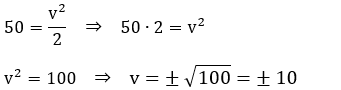
v = 10 m/s
Exercícios
1 - (PUC-MG) Os gatos conseguem sair ilesos de muitas
quedas. Suponha que a maior velocidade que ele possa atingir o solo, sem se
machucar, seja de 29 km/h. Então, desprezando-se a resistência do ar e
considerando g=10 m/s2, a altura máxima de queda para que
um gato, partindo do repouso, nada sofra é, aproximadamente, de:
a) 6,4 m
b) 10 m
c) 2,5 m
d) 3,2 m
e) 8,2 m
Resolução:
v = 29 km/h = 29:3,6 m/s ≅ 8,06 m/s
Energia mecânica do gato na altura
máxima:
v0 = 0
Em
= EC + Ep

Energia mecânica do gato no solo:
h = 0
Ems
= EC + Ep

Em = Ems


2 - (Ifba) O Beach Park, localizado em Fortaleza-CE, é o maior parque aquático da América Latina situado na beira do mar. Uma das suas principais atrações é um toboágua chamado “Insano”. Descendo esse toboágua, uma pessoa atinge sua parte mais baixa com velocidade módulo 28 m/s.
Considerando-se a aceleração da gravidade com módulo g = 10
m/s² e desprezando-se os atritos, estima-se que a altura do toboágua, em
metros, é de:
a) 28
b) 274,4
c) 40
d) 2,86
e) 32
Resolução:
v = 28 m/s
Energia mecânica na sua altura máxima do toboágua:
v0 = 0
Em
= EC + Ep

Energia mecânica no solo:
h = 0
Ems
= EC + Ep
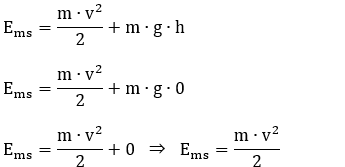
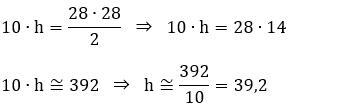
3 - (Ufes 2012) Um bloco de massa 0,10 kg é abandonado, a partir do repouso, de uma altura h de 1,2 m em relação a uma mola ideal de constante elástica 0,10 N/cm. Como é mostrado na figura rotulada como “Depois”, ao lado, o bloco adere à mola após o choque. No desenho, A é o ponto de abandono do bloco, B é o ponto de equilíbrio da mola, e C é o ponto onde há maior compressão da mola. Despreze perdas de energia por atrito e adote g = 10 m/s2.

A) Identifique, em um diagrama, as forças que atuam no
corpo, quando a deformação da mola é máxima.
B) Determine a velocidade do bloco imediatamente antes de se
chocar com a mola.
C) Determine o trabalho realizado sobre o bloco pela força
gravitacional entre os pontos A e B.
D) Determine a deformação máxima sofrida pela mola.
Quando necessário, utilize a aceleração da gravidade g = 10
m/s² e a constante universal dos gases R = 8,31 J/mol⋅K.
Resolução:
A)


C) 𝝉P =m⋅g⋅h
D) m = 0,10 kg
h = 1,2 m
Para converter N/cm para N/m, multiplicamos por 100:
A energia mecânica inicial no ponto A é puramente potencial
gravitacional:
A energia mecânica final no ponto C (compressão máxima) é
puramente potencial elástica:
Pela conservação da energia:



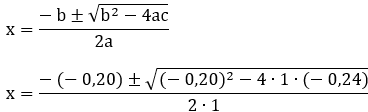

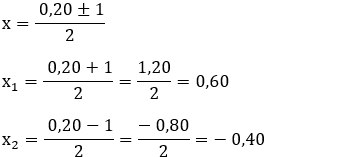
Resposta: x = 0,60 m ou x = 60 cm
4 - (Ifsp) Um atleta de salto com vara, durante sua corrida para transpor o obstáculo a sua frente, transforma a sua energia _____________ em energia ____________ devido ao ganho de altura e consequentemente ao/à _____________ de sua velocidade.
As lacunas do texto acima são, correta e respectivamente, preenchidas por:
a) potencial – cinética – aumento.
b) térmica – potencial – diminuição.
c) cinética – potencial – diminuição.
d) cinética – térmica – aumento.
e) térmica – cinética – aumento.
Resolução:
Frase corretamente preenchida:
Um atleta de salto com vara, durante sua corrida para transpor o obstáculo a sua frente, transforma a sua energia cinética em energia potencial devido ao ganho de altura e consequentemente ao/à diminuição de sua velocidade.
Resposta: Letra C
5 - (PUC-MG) Um ciclista desce uma rua inclinada, com forte vento contrário ao seu movimento, com velocidade constante. Pode-se afirmar que:
a) sua energia cinética está aumentando.
b) sua energia potencial gravitacional está diminuindo
c) sua energia cinética está diminuindo.
d) sua energia potencial gravitacional é constante.
Resolução:
Como a velocidade do ciclista é constante, a sua energia cinética também será, além disso, se ele desce a rua, a sua altura está diminuindo, então a sua energia potencial gravitacional também diminuirá.
Resposta: Letra B